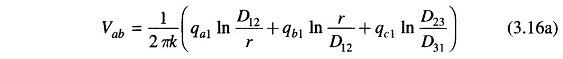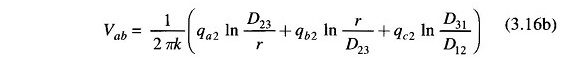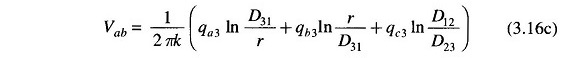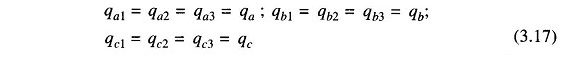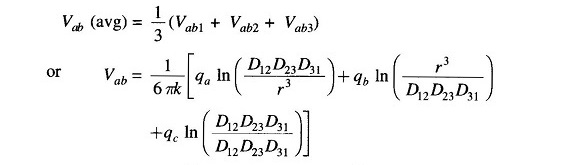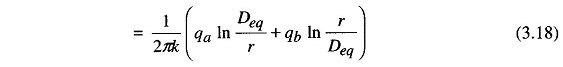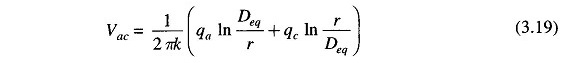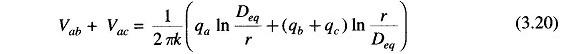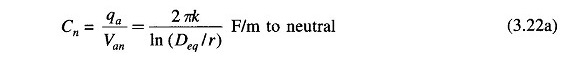Capacitance of Three Phase Line with Unsymmetrical Spacing:

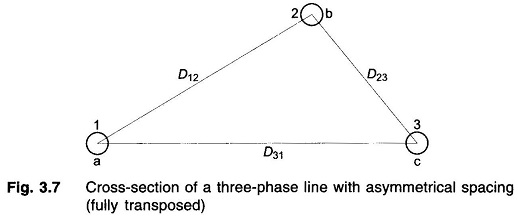
Figure 3.7 shows the three identical conductors of radius r of a Capacitance of Three Phase Line with Unsymmetrical Spacing. It is assumed that the line is fully transposed. As the conductors are rotated cyclically in the three sections of the transposition cycle, correspondingly three expressions can be written for V_ab. These expressions are:

For the first section of the transposition cycle

For the second section of the transposition cycle

For the third section of the transposition cycle

If the voltage drop along the line is neglected, V_ab is the same in each transposition cycle. On similar lines three such equations can be written for V_bc = V_ab ∠ –120°. Three more equations can be written equating to zero the summation of all line charges in each section of the transposition cycle. From these nine (independent) equations, it is possible to determine the nine unknown charges. The rigorous solution though possible is too involved.

With the usual spacing of conductors sufficient accuracy is obtained by assuming

This assumption of equal charge/unit length of a line in the three sections of the transposition cycle requires, on the other hand, three different values of V_ab designated as V_ab1, V_ab2 and V_ab3 in the three sections. The solution can be considerably simplified by taking V_ab as the average of these three voltages, i.e.

where

Similarly,

Adding Eqs. (3.18) and (3.19), we get

As per Eq. (3.12) for balanced three-phase voltages

and also

Use of these relationships in Eq. (3.20) leads to

The capacitance of line to neutral of the transposed line is then given by

For air medium (k_r = 1)

It is obvious that for equilateral spacing D_eq = D, the above (approximate) formula gives the exact result presented earlier.

The line charging current for a Capacitance of Three Phase Line with Unsymmetrical Spacing in phasor form is