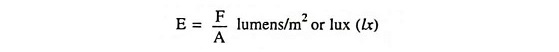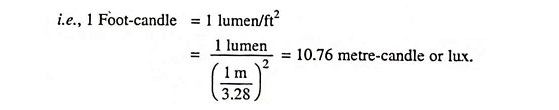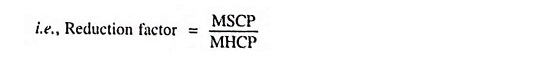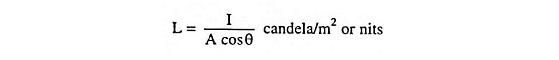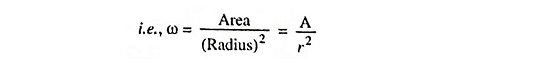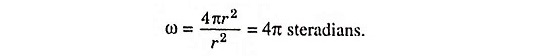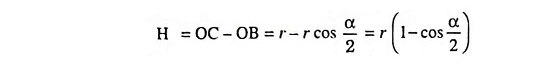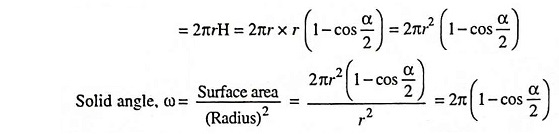What is illumination? – Terms used in Illumination

Light is the prime factor in the human life as all activities of human beings ultimately depend upon the light. Where there is no natural light, use of artificial light is made. Artificial lighting produced electrically, on account of its cleanliness, ease of control, reliability, steady output, as well as its low cost, is playing an increasingly important part in modern everyday life. Apart from its aesthetic and decorative aspects, good lighting has a strictly utilitarian value in increasing production, reducing workers fatigue, protecting their health, eyes and nervous system, and reducing accidents. The science of illumination engineering is, therefore, becoming of major importance.

Nature of Light: Light is a form of radiant energy. Various forms of incandescent bodies are the sources of light and the light emitted by such bodies depend upon the temperature of bodies. Heat energy is radiated into the medium by a body which is hotter than the medium surrounding it. The heat of the body, as seen, can be classified as red-hot or white-hot. While the body is red-hot the wavelength of radiated energy will be sufficiently large and the energy available is in the form of heat. When the temperature increases the body changes from red-hot to white-hot state, the wavelength of the energy radiated becomes smaller and enters into the range of the wavelength of light.

Actually the hot bodies emit heat as well as light energy, the velocity of these being equal to 3 x 10⁸ m/s. The light waves have wavelengths varying from 0.00075 mm to 0.0004 mm. The wavelength of light is usually expressed in Angstrom ; 1 Angstrom being equal to 10^-10 metre. The ratio of the energy emitted by the body in the form of light to the total energy emitted by the body is known as the ‘radiant efficiency‘ of the body, which depends upon the temperature. Higher the temperature of the body ; lower the wavelength of the radiant energy and higher the radiant efficiency. The radiant efficiency will be maximum when the temperature of the body will be such that the wavelength of the shortest wave radiated by the body is 0.0004 mm (4,000 Å). It is found that maximum radiant efficiency would occur at about 6,250°C and even then it would be 20%. Since this temperature is far above the highest that has yet been obtained in practice, it is obvious that the actual efficiency of all artificial light sources, i.e., those depending upon the temperature of incandescence is quite low.

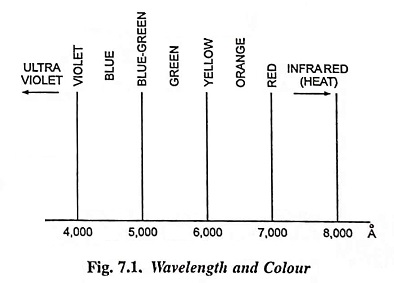
Colour: The sensation of colour is due to the difference in the wavelengths of the light radiations. Visible light can have a wavelength between 4,000 Å and 7,500 Å and the colour varies in the way, as shown in Figs. 7.1 and 7.2.

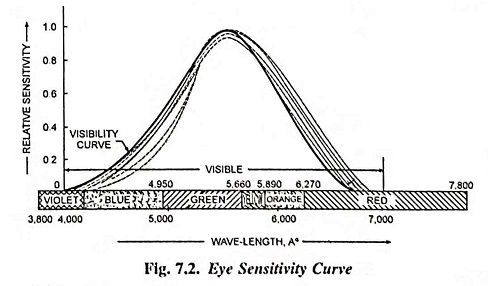
Relative Sensitivity: The sensitivity of the eye to the lights of different wavelengths varies from person to person and according to the age. The average relative sensitivity is shown in Fig. 7.2. The eye has greatest sensitivity for wavelengths of about 5,500 Å ; that is, yellow-green can be seen under poor conditions of illumination when blue or red cannot be seen under dim illumination, the sensitive curve tends to shift, as shown by the shaded region in Fig. 7.2. Therefore, violet disappears first and red remains visible. Yellow disappears last as the illumination becomes very dim. As each colour disappears, it becomes a grey shade, and finally black. The sensitivity of the eye to yellow-green radiation is taken as unity or 100% and the sensitivity to other wavelengths is expressed as a fraction or percentage of it. The relative sensitivity at any particular wavelength λ is written Kλ and is known as relative luminosity factor.

Illumination differs from light very much, though generally these terms are used more or less synonymously. Strictly speaking light is the cause and illumination is the result of that light on surfaces on which it falls. Thus the illumination makes the surface look more or less bright with a certain colour and it is this brightness and colour which the eye sees and interprets as something useful, or pleasant or otherwise.

Light may be produced by passing electric current through filaments as in the incandescent lamps, through arcs between carbon or metal rods, or through suitable gases as in neon and other gas tubes. In some forms of lamps the light is due to fluorescence excited by radiation arising from the passage of electric current through mercury vapour.

Some bodies reflect light in some measure, and when illuminated from an original source they become secondary sources of light. A good example is the Moon, which illuminates the earth by means of the reflected light originating in the Sun.

Terms used in Illumination:

The devising of modern lighting schemes and the selection of fittings and types of lamps requires a knowledge of the terms and quantities in general use for such purposes. Therefore, the following definitions are given in simple form to facilitate easy identification and reference.

(1) Light: It is defined as the radiant energy from a hot body which produces the visual sensation upon the human eye. It is usually denoted by Q, expressed in lumen-hours and is analogous to watt-hours.

(2) Luminous Flux: It is defined as the total quantity of light energy emitted per second from a luminous body. It is represented by symbol F and is measured in lumens (or cd-sr). The conception of luminous flux helps us to specify the output and efficiency of a given light source.

(3) Luminous Intensity: Luminous intensity in any given direction is the luminous flux emitted by the source per unit solid angle, measured in the direction in which the intensity is required. It is denoted by symbol I and is measured in candela (cd) or lumens per steradian.

If F is the luminous flux radiated out by source within a solid angle of ω steradians in any particular direction then I = F/ω lumens/steradian or candela (cd).

(4) Lumen: The lumen is the unit of luminous flux and is defined as the amount of luminous flux given out in a space represented by one unit of solid angle by a source having an intensity of one candle power in all directions.

i.e.,  Lumens = Candle power x solid angle = CP x ω

or total lumens given out by source of one candela is 4π lumens.

(5) Candle Power: Candle power is the light radiating capacity of a source in a given direction and is defined as the number of lumens given out by the source in a unit solid angle in a given direction. It is denoted by symbol CP.

(6) Illumination: When the light falls upon any surface, the phenomenon is called the illumination. It is defined as the number of lumens, falling on the surface, per unit area. It is denoted by symbol E and is measured in lumens per square metre or lux or metre-candle.

If a flux of F lumens falls on a surface of area A, then the illumination of that surface is

(7) Lux or Metre-Candle: It is the unit of illumination and is defined as the luminous flux falling per square metre on the surface which is everywhere perpendicular to the rays of light from a source of one candle power and one metre away from it.

(8) Foot-Candle: It is also the unit of illumination and is defined as the luminous flux falling per square foot on the surface which is everywhere perpendicular to the rays of light from a source of one candle power and one foot away from it.

(9) Candela: It is the unit of luminous intensity. It is defined as 1/60th of the luminous intensity per cm² of a black body radiator at the temperature of solidification of platinum (2,043 K).

(10) Mean Horizontal Candle Power (MHCP): It is defined as the mean of candle powers in all directions in the horizontal plane containing the source of light.

(11) Mean Spherical Candle Power (MSCP): It is defined as the mean of candle powers in all directions and in all planes from the source of light.

(12) Mean Hemispherical Candle Power (MHSCP): It is defined as the mean of candle powers in all directions above or below the horizontal plane passing through the source of light.

(13) Reduction Factor: Reduction factor of a source of light is the ratio of its mean spherical candle power to its mean horizontal candle power.

(14) Lamp Efficiency: It is defined as the ratio of the lumi­nous flux to the power input. It is expressed in lumens per watt.

(15) Specific Consumption: It is defined as the ratio of the power input to the average candle power. It is expressed in watts per candela.

(16) Brightness or Luminance: When the eye receives a great deal of light from an object we say it is bright, and ‘brightness’ is an important quantity in illumination. It is all the same whether the light is produced by the object or merely reflected from it. The object sends out light as though each small piece of its surface were of a certain luminous intensity. Generally, the brightness of an object is not the same from all points of view. When brightness is considered in terms of measurable quantity, the term luminance is employed.

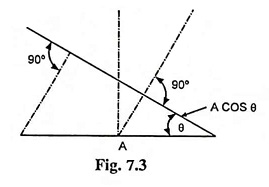
Brightness or luminance is defined as the luminous intensity per unit projected area of either a surface source of light or a reflecting surface and is denoted by L.

If a surface of area A has an effective luminous inten­sity of I candelas in a direc­tion θ to the normal, then the luminance (brightness) of that surface is

i.e., nit is defined as candela per square metre. Bigger unit of luminance is stilb which is defined as candelas per square cm. Lambert is also the unit of brightness which is lumens/cm². Foot-lambert is lumens/ft².

(17) Glare: The size of the opening of the pupil in the human eye is controlled by its iris. If the eye is exposed to a very bright source of light, the iris automatically contracts in order to reduce to amount of light admitted and prevent damage to retina ; this reduces the sensitivity, so that other objects within the field of vision can be only imperfectly seen. This effect is referred to ‘glare’ and is familiar in connection with motor-car headlights. In other words glare may be defined as the brightness within the field of vision of such a character as to cause annoyance, discomfort, interference with vision or eye fatigue.

(18) Space-height Ratio: It is defined as the ratio of horizontal distance between adjacent lamps and height of their mountings.

(19) Utilization Factor or Coefficient of Utilization: It is defined as the ratio of total lumens reaching the working plane to total lumens given out by the lamp.

(20) Maintenance Factor: Due to accumulation of dust, dirt and smoke on the lamps, they emit less light than that they emit when they are new ones and similarly the walls and ceilings, etc., after being covered with dust, dirt and smoke do not reflect the same output of light, which is reflected when they are new.

The ratio of illumination under normal working conditions to the illumination when the things are perfectly clean is known as maintenance factor.

(21) Depreciation Factor: This is merely the inverse of the maintenance factor and is defined as the ratio of initial metre- candles to the ultimate maintained metre-candles on the working plane. Its value is more than unity.

(22) Waste Light Factor: Whenever a surface is illuminated by a number of sources of light, there is always a certain amount of waste of light on account of overlapping and falling of light outside the edges of the surface. The effect is taken into account by multiplying the theoretical value of lumens required by 1.2 for rectangular areas and 1.5 for irregular areas and objects such as statues, monuments etc.

(23) Absorption Factor: In the places where atmosphere is full of smoke fumes, such as in foundries, there is a possibility of absorption of light. The ratio of total lumens available after absorption to the total lumens emitted by the source of light is called the absorption factor. Its values varies from unity for clean atmosphere to 0.5 for foundries.

(24) Beam Factor: The ratio of lumens in the beam of a projector to the lumens given out by lamps is called the beam factor. This factor takes into account the absorption of light by reflector and front glass of the projector lamp. Its value varies from 0.3 to 0.6.

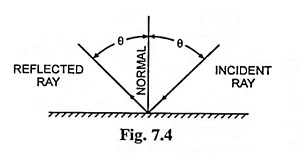
(25) Reflection Factor: When a ray of light impinges on a surface it is reflected from the surface at an angle of incidence, as shown in Fig. 7.4. A certain portion of incident light is absorbed by the surface. The ratio of reflected light to the incident light is called the ‘reflection factor‘. It is always less than unity.

(26) Solid Angle: Plane angle is subtended at a point in a plane by two converging straight lines and its magnitude is given by

The largest angle sub­tended at a point is 2π radians.

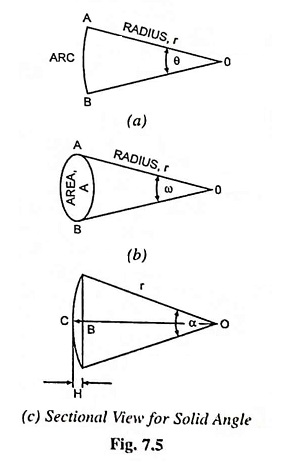
Solid angle is the angle generated by the surface passing through the point in space and the periphery of the area. Solid angle is denoted by ω, expressed in steradians and is given by the ratio of the area of the surface to the square of the distance between the area and the point.

The largest solid angle subtended at a point is that due to a sphere at its centre. If r is the radius of any sphere, its surface area is 4πr² and the distance of its surface area from the centre is r, therefore, solid angle subtended at its centre by its surface,

Relationship between plane and solid angle can be obtained as follows.

Consider a curved surface of a spherical segment of height H and radius r [Fig. 7.5. (c)].

Surface area of such a segment = 2πrH

From Fig. 7.5 (c)

Surface area of the surface under consideration

Thus solid angle subtended at a point can be determined directly from the above relation knowing the plane angle subtended by its section.

(27) Steradian: It is the unit of solid angle and is defined as the solid angle that subtends a surface on the sphere equivalent to the square of the radius.