Fast Fourier Transform Interview Questions and Answers:
1. Why FFT is needed?
Ans. The direct evaluation of DFT using the formula
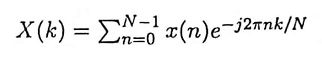
requires N2 complex multiplications and N(N – 1) complex additions. Thus for reasonably large values of N (in order of 1000) direct evaluation of the DFT requires an inordinate amount of computation. By using FFT algorithms the number of computations can be reduced. For example, for an N-point DFT, the number of complex multiplications required using FFT is N/2 log2N. If N = 16, the number of complex multiplications required for direct evaluation of DFT is 256, whereas using DFT only 32 multiplications are required.
2. What is the main advantage of FFT?
Ans. FFT reduces the computation time required to compute discrete Fourier transform.
3. What is FFT?
Ans. The fast Fourier transform (FFT) is an algorithm used to compute the DFT. It makes use of the symmetry and periodicity properties of twiddle factor WkN to effectively reduce the DFT computation time. It is based on the fundamental principle of decomposing the computation of DFT of a sequence of length N into successively smaller discrete Fourier transforms. The FFT algorithm provides speed-increase factors, when compared with direct computation of the DFT, of approximately 64 and 205 for 256-point and 1024-point transforms, respectively.
4. How many multiplications and additions are required to compute N-point DFT using radix-2 FFT?
Ans. The number of multiplications and additions required to compute N-point DFT using radix-2 FFT are Nlog2N and N/2log2N respectively.
5. What is meant by radix-2 FFT?
Ans. The FFT algorithm is most efficient in calculating N-point DFT. If the number of output points N can be expressed as a power of 2, that is, N = 2M, where M is an integer, then this algorithm is known as radix-2 FFT algorithm.
6. What is a decimation-in-time algorithm?
Ans. Decimation-in-time algorithm is used to calculate the DFT of a N-point sequence. The idea is to break the N-point sequence into two sequences, the DFTs of which can be combined to give the DFT of the original N-point sequence. Initially the N-point sequence is divided into two N/2-point sequences
xe(n) and xo(n), which have the even and odd members of x(n) respectively. The N/2-point DFTs of these two sequences are evaluated and combined to give the N-point DFT. Similarly the N/2-point DFTs can be expressed as a combination of N/4-point DFTs. This process is continued until we left with 2-point DFT. This algorithm is called decimation-in-time because the sequence x(n) is often splitted into smaller subsequences.
7. What is Decimation-in-frequency algorithm?
Ans. It is a popular form of the FFT algorithm. In this the output sequence X(k) is divided into smaller and smaller subsequences, that is why the name decimation in frequency. Initially the input sequence x(n) is divided into two sequences x1(n) and x2(n) consisting of the first N/2-samples of x(n) and the last N/2-samples of x(n) respectively. Then, we find the N/2-point sequences f(n) and g(n) as
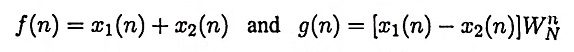
The N/2-point DFTs of the above two sequences give even membered and odd membered output samples respectively.
The above procedure can now be iterated to express each N/2-point DFT as a combination of two N/2-point DFTs. This process is continued until we left with 2 point DFT.
8. What are the differences and similarities between DIF and DIT algorithms?
Ans.
Differences:
For DIT, the input is bit reversal while the output is in natural order, whereas for DIF, the input is in natural order while the output is bit reversed.
The DIF butterfly is slightly different from the DIT butterfly, the difference being that the complex multiplication takes place after the add-subtract operation in DIF.
Similarities:
Both algorithms require same number of operations of compute the DFT. Both algorithms can be done in-place and both need to perform bit reversal at some place during the computation.
9. What is the basic operation of DIT algorithm?
Ans. The basic operation of DIT algorithm is the so called butterfly in which two inputs Xm(p) and Xm(q) are combined to give the outputs Xm+1(p) and Xm+1(q) via. the operation
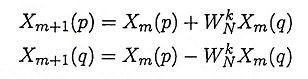
where WkN is twiddle factor.
10. What is the basic operation of the DIF algorithms?
Ans. The basic operation of the DIF algorithm is the so called butterfly in which two inputs Xm(p) and Xm(q) are combined to give the outputs Xm+1(p) and Xm+1(q) via the operation
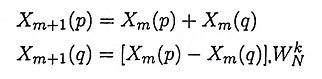
where WkN is twiddle factor.
11. Draw the flow graph of a two point DFT for a decimation-in-time decomposition.
Ans. The flow graph of a two-point DFT for a decimation-in-time algorithm is
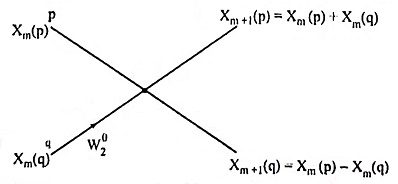
where Xm(p) and Xm(q) are inputs to the butterfly, Xm+1(p) and Xm+1(q) are outputs of the butterfly. The nodes p and q represents memory locations.
12. Draw the flow graph of a two-point radix-2 DIF-FFT
Ans. The flow graph of a two-point DFT for a decimation-in-time frequency algorithm is
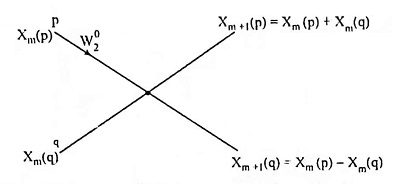
where Xm(p) and Xm(q) are inputs, Xm+1(p) and Xm+1(q) are outputs of the butterfly. The nodes p and q represents memory locations.
13. Draw the basic butterfly diagram for DIT algorithm.
Ans. The basic butterfly diagram for DIT algorithm is
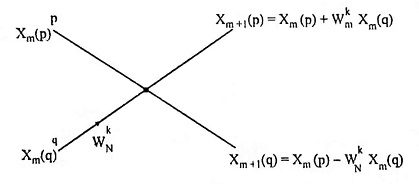
where Xm(p) and Xm(q) are inputs to the butterfly, Xm+1(p) and Xm+1(q) are outputs of the butterfly. The nodes p and q represents memory locations.
14. Draw the basic butterfly diagram for DIF algorithm.
Ans. The basic butterfly diagram for DIF algorithm is
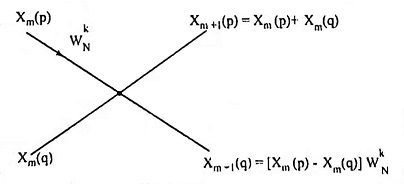
where Xm(p) and Xm(q) are inputs, Xm+1(p) and Xm+1(q) are outputs of the butterfly. The nodes p and q represents memory locations.
15. What is meant by ‘in-place’ in DIT and DIF algorithms?
Ans. The basic butterfly diagrams used in DIT and DIF algorithms are shown in Fig.1 and Fig. 2 respectively.
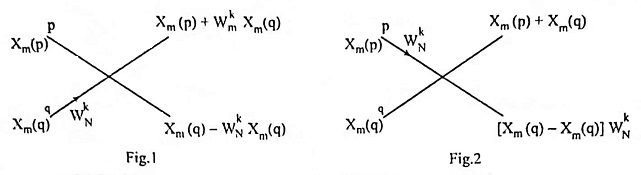
In Fig. 1 two lines emerging from two nodes cross each other and connected to two nodes on the right hand side. These nodes represents memory locations. At the input nodes Xm(p) and Xm(q), the inputs are stored. After the outputs Xm+1(p) and Xm+1(q) are calculated, the same memory location is used to store the new values in place of the input values. An algorithm that use the, same location to store both the input and output sequences is called an ‘in-place’ algorithm.
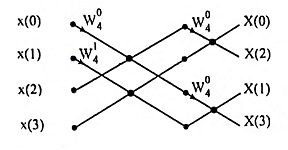
16. Draw the 4-point radix-2 DIF-FFT butterfly structure for DFT.
Ans.
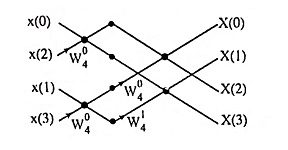
17. Draw the 4-point radix-2 DIT-FFT butterfly structure for DFT
Ans.
18. What are the applications of FFT algorithms?
Ans. The applications of FFT algorithm includes
- Linear filtering,
- Correlation,
- Spectrum analysis.