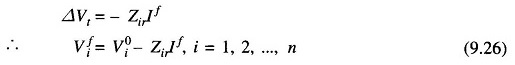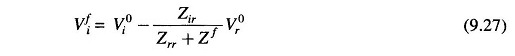Algorithm for Short Circuit Computation:

So far we have carried out short circuit calculations for simple systems whose passive networks can be easily reduced. In this section we extend our study to large systems. In order to apply the four steps of Algorithm for Short Circuit Computation developed earlier to large systems, it is necessary to evolve a systematic general algorithm so that a digital computer can be used.

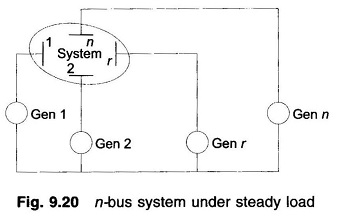
Consider an n-bus system shown schematically in Fig. 9.20 operating at steady load. The first step towards Short Circuit Computation is to obtain prefault voltages at all buses and currents in all lines through a load flow study. Let us indicate the prefault bus voltage vector as

Let us assume that the rth bus is faulted through a fault impedance Z^f. The postfault bus voltage vector will be given by

where

• ΔV is the vector of changes in bus voltages caused by the fault.

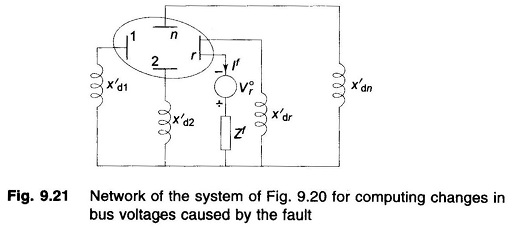
As step 2, we drawn the passive Thevenin network of the system with generators replaced by transient/subtransient reactances with their emfs shorted (Fig. 9.21).

As per step 3 we now excite the passive Thevenin network with – V°_r in series with Z^f as in Fig. 9.21. The vector ΔV comprises the bus voltages of this network.

Now

Where

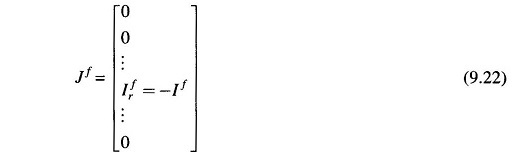
Since the network is injected with current -I^f only at the rth bus, we have

Substituting Eq. (9.22) in Eq. (9.20), we have for the rth bus

By step 4, the voltage at the rth bus under fault is

However, this voltage must equal

We have from Eqs. (9.23) and (9.24)

At the ith bus (from Eqs (9.20) and (9.22))

substituting for I^f from Eq. (9.25), we have

For i = r in Eq. (9.27)

In the above relationship V_i^0,s, the prefault bus voltages are assumed to be known from a load flow study. Z_BUS matrix of the short-circuit study network of Fig. 9.21 can be obtained by the inversion of its Y_BUS matrix or the Z_BUS building algorithm. It should be observed here that the SC study network of Fig. 9.21 is different from the corresponding load flow study network by the fact that the shunt branches corresponding to the generator reactances do not appear in the load flow study network. Further, in formulating the SC study network, the load impedances are ignored, these being very much larger than the impedances of lines and generators. Of course synchronous motors must be included in Z_BUS formula­tion for the SC study.

Postfault currents in lines are given by

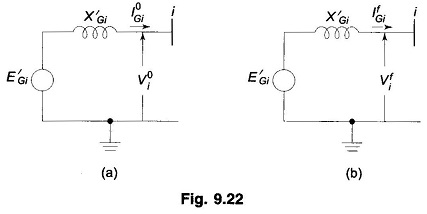
For calculation of postfault generator current, examine Figs. 9.22(a) and (b). From the load flow study (Fig. 9.22(a))

Prefault generator output = P_Gi + jQ_Gi

From the SC study, V^f_i is obtained, It then follows from Fig. 9.22(b) that