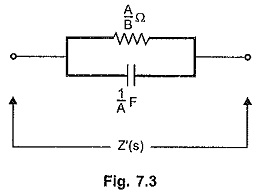
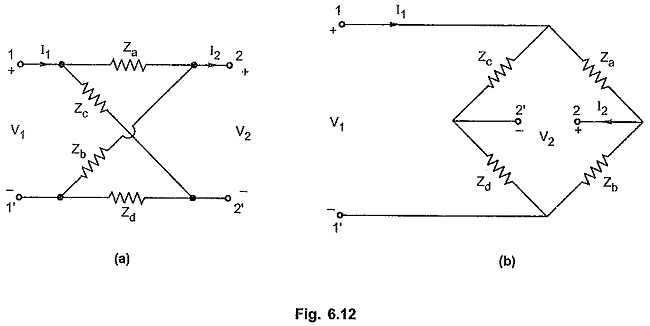
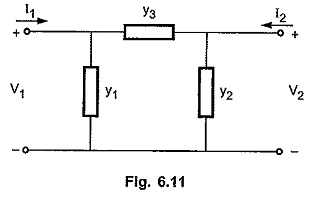
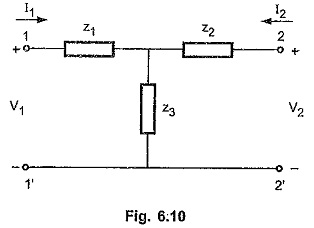
Driving Point Immittance Function: The immitance function must be positive real function so that its synthesis can be done to obtain an electrical network, using passive elements. We have discussed the tests to confirm the…
Positive Real Function: Let us study another class of functions called positive real functions. The significance of positive real functions is that if the driving point immitance (i.e. admittance or impedance) is a positive real…
Hurwitz Polynomial: For a polynomial P(s) to be a Hurwitz polynomial, it has to satisfy following basic properties, The polynomial P(s) is real when 's' is real. The roots of the polynomial P(s) have real…
Realisability of One Port Network: Realisability of One Port Network - Consider the network function H(s) which is the ratio of Laplace transform of the output R(s) to the Laplace transform of the excitation E(s).…
Elements of Network Synthesis: Elements of Network Synthesis - For any network, three things are associated with it. These are network elements, input i.e. excitation to the network and output i.e. response from the network.…
Transfer Function of Terminated Two Port Network: A ratio of voltage or current at one port to the voltage or current at the other port is called a Transfer Function of Terminated Two Port Network.…
Bridged T Network Analysis: Consider Bridged T Network Analysis as shown in the Fig. 6.15 (a). We can consider bridged T network as a parallel connection of the two networks as shown in the Fig.…
Lattice Network: The lattice network is one of the common four terminal networks. These networks are generally used in filter sections and also used as symmetrical attenuators. Consider the lattice network shown in the Fig.…
π or pi Network in Network Analysis: Consider following two port ’π’ or pi Network type network with assumed voltages V1 and V2 and current I1 end I2 as shown in Fig. 6.11. Let the…
T Network: Consider two port T Network with assumed voltages V1 and V2 and currents I1 and I2 as shown in Fig. 6.10. Let the z-parameters of the above network are represented as follows We…
