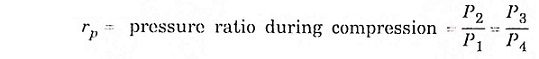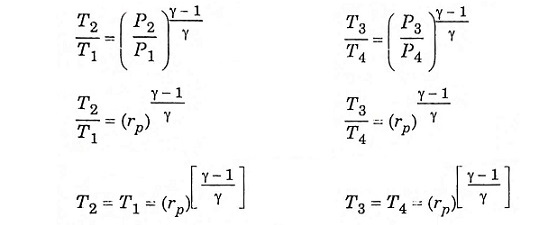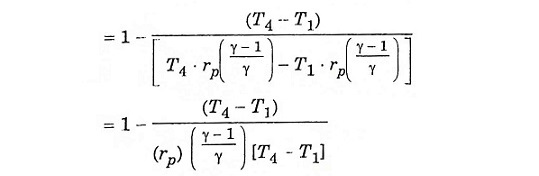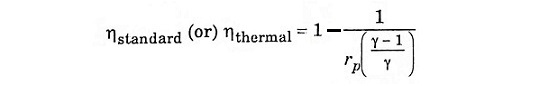Brayton Cycle – Process, PV Diagram and TS Diagram:

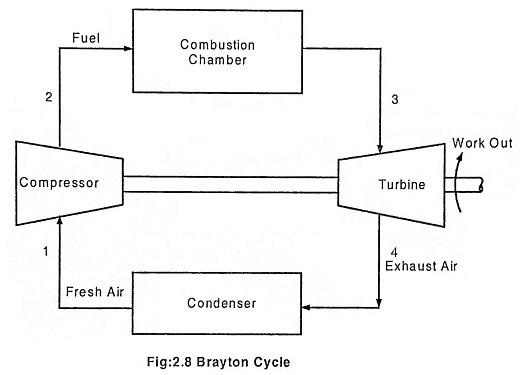
The Brayton cycle represents the operation of a gas turbine engine. The cycle consists of four processes. This cycle was invented by an American Engineer George Baily Brayton. Brayton cycle describes the working of a constant pressure heat engine. Gas turbine and air breathing jet engine use the Brayton cycle. Although the Brayton cycle is usually run as a open cycle system, it is conventual assumed for the purpose of thermodynamic analysis that the exhaust gases are reused in the intake, therefore enabling analysis as a closed system.

The main components of a gas turbine are:

1. Compressor
2. Combustion chamber
3. Turbine
4. Condenser

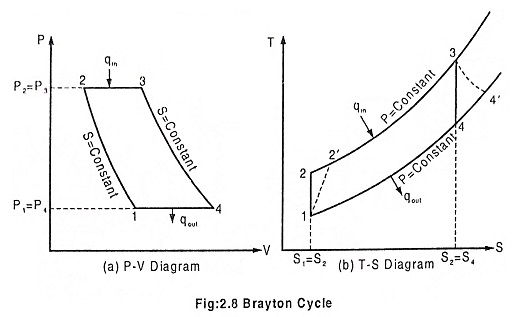
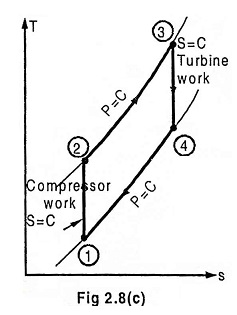
Process 1 – 2 Isentropic compression

The ambient air is drawn to the compressor and is pressurized or compressed from pressure P₁ to P₂. The temperature increases from T₁ to T₂, volume reduces from V₁ to V₂ with the entropy being constant.

Process 2 – 3 Heat addition at constant pressure

The compressed air then runs through a combustion chamber, where fuel is burned, heat is added at constant pressure P₂ = P₃. Temperature rises from T₂ to T₃ Due to the combustion, volume increases from V₂ to V₃ and the entropy also increases from S₂ to S₃.

Process 3 – 4 Isentropic expansion

The heated, pressurized air then gives up its energy by expanding through a turbine. The work extracted by the turbine is used to drive the compressor which is coupled to it. The pressure decreases from P₃ to P₄. Temperature decreases from T₃ to T₄. Volume slightly increases from V₃ to V₄, and the entropy remains constant S₃ = S₄.

Process 4 – 1 Heat rejection at constant pressure

In an open Brayton cycle the exhaust air is released to the atmosphere and fresh air is drawn by the compressor for the next cycle, where as in closed Brayton cycle, the exhaust air is condensed in a condenser and then redrawn by the compressor. Heat is rejected at constant pressure P₄ = P₁ in both the cases. The temperature decreases from T₄ to T₁, volume decreases from V₄ to V₁ and the entropy decreases from S₄ to S₁.

Thermal efficiency of the cycle

Heat supplied at constant pressure = m C_p (T₃ – T₂)

Heat rejected at constant pressure = m C_p (T₄ – T₁)

Process (1) – (2) isentropic process  (3) – (4) isentropic process

Substitute T₂ and T₃ in eqn (1), we get η_{Air standard} (or) η_thermal