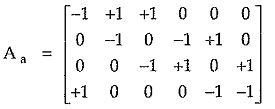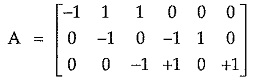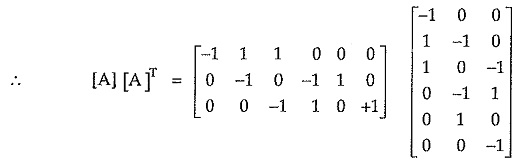Define Incidence Matrix:

Define Incidence Matrix consists of two parts, namely

1. Complete Incidence Matrix
2. Reduced Incidence Matrix

Complete Incidence Matrix (A_a):

Define Incidence Matrix is nothing but a mathematical model to represent the given network with all the information available. The information regarding the network is nothing but which branches are incident at which node and what are the orientations relative to the nodes. All this information is written in a matrix form which is called complete incidence matrix. It is represented by A_a.

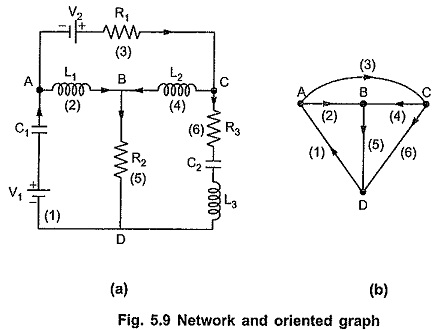
Consider following network and its oriented graph as shown in Fig. 5.9.

There are 4 nodes A, B, C, D and 6 branches as 1, 2, 3, 4, 5 and 6. The directions are selected randomly for explanation purpose. For a graph , if there are ‘n’ nodes and ‘b’ branches, the complete incidence matrix A_a = a_hk is a rectangular matrix of order n x b. The standard conventions to be followed while writing the incidence matrix are as given below

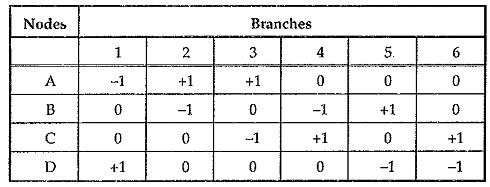
The complete incidence matrix of the network shown in Fig. 5.9 (b) is as given below in the tabular form.

Nodes = A, B, C, D

Branches = 1, 2, 3, 4, 5, 6

The above result can be written in matrix form as follows,

In above matrix, the summation of elements in any column results in zero value. This is because each of the branch is considered in one column. Each branch connects two nodes. The current flows towards the node at one end of the branch, while it flows away from the node at other end.

Any one row of the complete incidence matrix can be obtained by algebraic manipulation of other rows. For example in above matrix, the fourth row is negative of sum of first three rows. At least we can eliminate one of the rows as that can be obtained by negative of sum of others.

Reduced Incidence Matrix:

When any one row from the complete incidence matrix is eliminated by using mathematical manipulations, then the matrix is called reduced incidence matrix (or simply the incidence matrix). It is denoted by simply A.

The reduced incidence matrix is always of the order (n – 1) x b . In the above problem, if 4th row is eliminated by the mathematical manipulations, then reduced incidence matrix is given as

For a given graph select a tree. In the incidence matrix, arrange the columns such that the first (n- 1) columns correspond to the twigs for the selected tree and last (b – n + 1) columns correspond to the links.

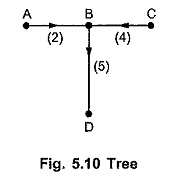
Suppose we select one tree as shown in Fig. 5.10.

Then reduced incidence matrix A can be written by writing columns corresponding to twigs first and columns corresponding to chords (links) after that.

The reduced incidence matrix can be written as,

where,

A_T is the square matrix of the order (n – 1) x (n – 1) whose columns corresponds to twigs, hence name of the matrix is A_T.

A_L is the matrix of the order (n – 1) x (b – n + 1) whose columns represents the links, hence name of the matrix is A_L.

The number of possible trees is given by following relation,

Properties of Complete Incidence Matrix :

Each row in the matrix corresponds to a node of the graph. Each row has non zero entries such as +1 and -1 depending upon the orientation of branch at the nodes. Also the entries in all other columns of that row are zero.

The properties are as follows.

1. The sum of the entries in any column is zero.
2. The rank of a complete incidence matrix of a connected (oriented) graph is (n -1).
3. The determinant of a loop of complete incident matrix is always zero.