Digital Codes Types:

Various Digital Codes Types of equipment are used in computer systems to send and receive data: keyboards, video terminals, printers, paper tape punches and readers, paper card punches and readers, and magnetic storage devices. Each of these types of equipment generates and receives data in the form of Digital Codes Types. The fact that all use encoded data, however, does not mean that all use the same code. Indeed, several Digital Codes Types exist and are common among digital data systems. The reasons for more than one encoding system are several.

Codes evolved during the development of data systems. Some of these codes replaced existing codes, but as new encoding systems developed, the previous systems continued alongside the new codes.

Standardization is not easy to accomplish. It is difficult to convert all users to a single coding scheme, since some codes are advantageous for one use although others are better for different applications. Adopting nationwide and especially worldwide standards is normally a lengthy and sometimes frustrating process. As in many other areas, the marketplace and politics make the ultimate decision.

The capability of modem data systems has reduced the necessity of establishing a single encoding scheme. Modern computers can easily deal with different Digital Codes Types by simply converting them to the code used by the computer. With speeds of several million operations per second for many current computers, the time invested in code translation is negligible. The result is that several encoding systems are in use within data systems and can be expected to continue in use for some time. It is necessary, therefore, that these major encoding systems be given due consideration.

The Baudot Code:

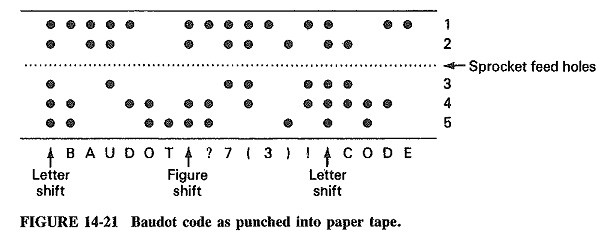
Named for the telegraph pioneer, J. M. E. Baudot, the Baudot code is a 5-bit code which has been used in telegraphy and paper-tape systems. With only 5 bits available, the basic code is limited to 32 different code combinations (5² = 32). Shift codes have been incorporated into the Baudot code to indicate whether a code is upper- or lowercase. This increases the number of code combinations to 64, of which 6 are used for function codes, leaving only 58 available codes. The alphabet, numbers and functions require 42 of these 58. This limits the ability of the Baudot code to provide extra punctuation and computing codes. Figure 14-20 shows the Baudot en­coding scheme. Another limitation of the Baudot code is evident in the figure: the code is not sequential, limiting its ability to be used for computation.

Early teletypewriter machines used the Baudot code for intercommunication. Many of these machines incorporated a paper-tape punch and reader mechanism in their systems. Figure 14-21 illustrates the use of a Baudot code with paper tape. The use of shift characters to indicate that succeeding characters are letters or figures is also shown.

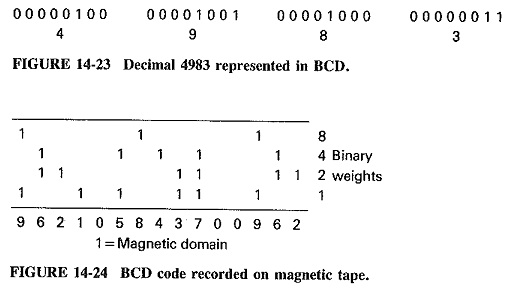
The binary code: Binary encoding forms the basis of several coding schemes. If straight binary encoding is used, 256 different combinations are possible for an 8-bit character. Binary encoding is not used unmodified in many situations, however, for several reasons. Although 256 combinations are available this is inadequate for representation of large numbers. Also, it was learned early that errors can occur during transmission of data, but the use of an unmodified 8-bit/binary code did not permit any means of error detection. The most useful Digital Codes Types would incorporate an error-detecting bit, called a parity bit. For use with numbers, the binary code was modified so that only the lower 4 bits were needed. This system, called binary-coded-decimal (BCD), counts binarily from 0 to 9, as shown in Figure 14-22. The sequence uses a second 8-bit word to represent each successive decimal column. As one binary word reaches decimal 10, it returns to zeros and a carry is added into the next binary word. The use of BCD encoding to represent a four-digit decimal number is shown in Figure 14-23.

One of the uses for BCD encoding is for data representation on magnetic tape. Data is recorded on magnetic tape in much the same way as audio; a recording head creates a magnetic patten on the tape which represents the information. For data recording, the recording is made on several tracks. A 1 results in a magnetized spot being recorded, while a 0 leaves the spot unmagnetized. For recording BCD, four tracks are used, with each character being represented by a pattern of magnetized spots on the track, similar to the holes in a punched tape (see Figure 14-24).

An extension of the BCD code is the 7-bit alphanumeric code. This Digital Codes Types uses BCD for representation of numbers, but adds two extra bits to represent letters and punctuation marks (see Figure 14-25). A seventh bit is used to provide parity for error detection. These 7 bits are recorded on seven parallel tracks on the magnetic tape.

ASCII Code:

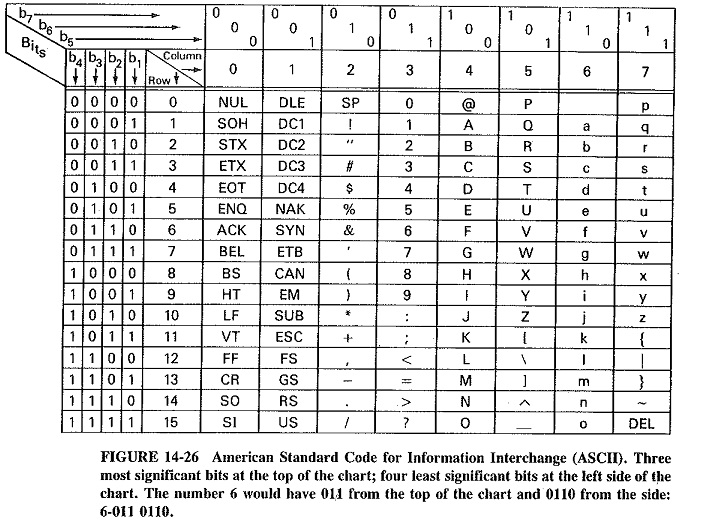
One of the more universal Digital Codes Types is the American Standard Code for Information Interchange (ASCII). ASCII is based on a binary progression, as demonstrated in Figure 14-26. It should be noted that the code is arranged so that the numbers are represented by a standard BCD progression within the last bits shown on the left of the chart, while the preceding 3 bits, shown at the top of the chart, specify whether a number, letter or character is being represented by the last 4 bits. For example, the table shows that an ASCII code of 0110001 represents the number 1, while 1000001 represents a capital “A,” and the code 1100001 represents a lowercase “a.” By using a standard binary progression, ASCII makes possible mathematical operations with numbers. Since the letters are also in a binary progression, alphabetizing can be accomplished by using simple binary mathematical procedures.

Most modern computers use hexadecimal notation internally. Hexadecimal notation represents a 4-bit binary word with one of 16 symbols (0,1,2,3,4,5,6,7,8, 9,A,B,C,D,E,F). An 8-bit word is easily accommodated in these computers. Since ASCII is a 7-bit code, it is normally converted into 8-bit words by using the most significant bit as a parity for error detection. Typically, the parity bit is given the value (1 or 0) which will result in the stun of the 1s in the ASCII data word being even. When checked after transmission, if the parity bit does not result in an even sum, an error is assumed and the data is retransmitted.

EBCDIC:

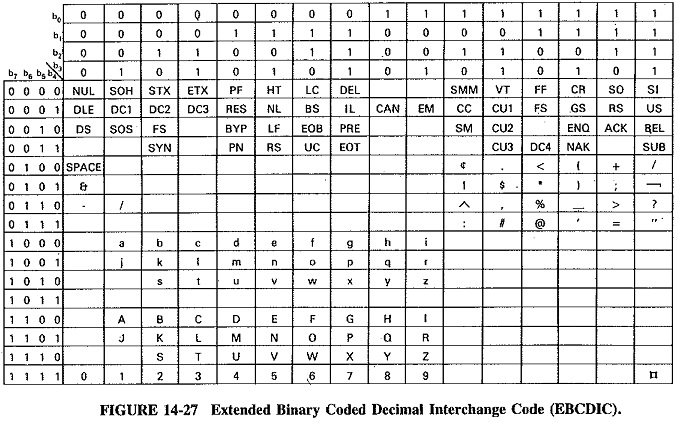
Another popular Digital Codes Types is called the Extended Binary Coded Decimal Interchange Code (EBCDIC). EBCDIC is also based on the binary-coded decimal format, as its name implies, but it differs from the ASCII code in several respects. As shown in Figure 14-27, EBCDIC uses all 8 bits for information, so that no parity bit is available. Also, although EBCDIC follows a BCD progression for the numbers, the numbers follow the letters rather than preceding them as they do in ASCII. Approved by the International Telephone and Telegraph Consultative Committee (CCITT), EBCDIC has similarities to the Baudot code.

Hollerith Code:

Several Digital Codes Types are in use for punched cards, many of them specific to particular manufacturers. One of the more universal punched-card codes is the Holler­ith code. This code is used with an 80-column card, as shown in Figure 14-28. It is seen that the code for a number, letter, punctuation or control character is punched into the card as a pattern of rectangular slots using variations of 12 horizontal rows. The logical arrangement of the Hollerith code makes it convenient for sorting and computing applications.