Digital Modulation Techniques:
An information bearing signal can be transmitted from one point to another point over a communication channel by using either an analog technique or digital modulation techniques. As already discussed, the use of digital technique offers several important advantages as compared to analog technique.
In particular, a digital communication system offers the following highly attractive features :
- Immunity to channel noise and external interference unmatched by any analog communication system.
- flexible operation of the system.
- Integration of diverse sources of information into a common format.
- Security of information during its transmission from source to the destination.
In view of the above reasons, digital communications have become the dominant form of communication technology in our society.
However, to handle the transmission of analog message signals (i.e. voice and video signals) by digital means, the signal has to undergo an analog-to-digital conversion. Using the waveform coding technique, the analog PAM signal is converted into a digital signal. This digital signal is in the form of a train of stream of binary digits 0 and 1. Thus, with waveform coding techniques, we enter into the world of digital communication. After sampling an analog signal, the next step in its digital transmission is the generation of the “coded version” (digital representation) of the signal. Pulse code modulation (PCM) provides one method to meet such a requirement.
In PCM, the message signal is sampled and amplitude of each sample is approximated (rounded off) to the nearest one of a finite set of discrete levels. This will enable us to represent both time and amplitude in discrete forms. Thus, it is possible to transmit the message signal by means of a digital (coded) waveform. Conceptually PCM is simple to understand. It was the first method which was developed for the digital coding of the waveforms. PCM is the most applied of all the digital coding systems in use today. PCM is therefore widely accepted as the standard against which the other digital coding systems are calibrated.
Discretization in Time and Amplitude:
As discussed earlier, pulse modulation may be classified as pulse analog modulation and pulse digital modulation. In the case of pulse analog modulation, only time is expressed in the digital form and any one of the pulse parameters (i.e. pulse amplitude, duration or position) is varied in a continuous manner in accordance with the message signal. In the pulse analog modulation schemes (PAM, PWM or PPM), information transmission is accomplished in an analog form at discrete times. On the other hand, in the pulse Digital Modulation Techniques, the time and the pulse parameter (usually the amplitude) occur in discrete form and digital coded form respectively. Pulse digital modulation techniques is therefore basically a scheme which converts the analog signal to its corresponding digital form. It is for this reason that the analog-to-digital conversion is sometimes known as pulse digital modulation.
The simplest form of pulse Digital Modulation Techniques is called the pulse coded modulation (PCM). In this system, the message signal is first sampled and then amplitude of each sample is rounded off to the nearest one of a finite set of allowable values known as quantization levels, so that both time and amplitude are in discrete form. Thus in PCM, both parameters i.e. time and amplitude are expressed in discrete form. This process is known as discretization in time and amplitude.
Concept of Quantization:
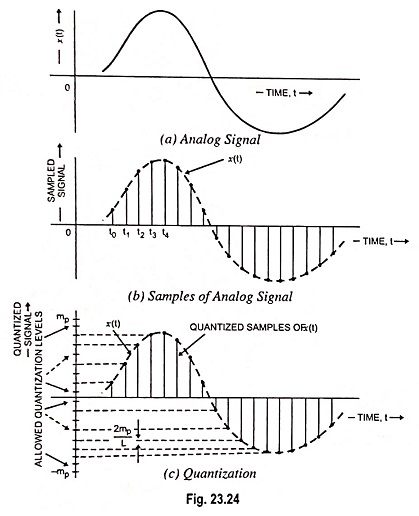
In communication systems, sometimes it happens that analog signal is available with us but we have to transmit it in digital form for a particular application. In such cases, analog signal is required to be converted into digital signal. It means that a continuous time signal is required to be converted in the form of digits. For understanding the process of converting a signal from analog to digital form, let us consider an analog signal, as shown in Fig. 23.24 (a). First of all, we get samples of the given signal according to sampling theorem. For this purpose, we mark the time instants t0, t1, t2, and so on, at equal time intervals along the time axis. At each of these time instants, the magnitude of signal is measured and thus samples of the signal are taken. Figure 23.24 (b) shows a representation of the signal of the Fig. 23.24 (a) in terms of its samples.
Now, it can be said that the signal in Fig. 23.24 (b) is defined only at the sampling instants. This means that it no longer is a continuous function of time, but rather, it is a discrete-time signal. However, since the magnitude of each sample can take any value in a continuous range, the signal in Fig. 23.24 (b) is still an analog signal. This difficulty is resolved by a process known as quantization. In quantization, the total amplitude range which the signal may occupy is divided into a number of standard levels.
As shown in Fig. 23.24 (c), amplitudes of the signal x(t) lie in the range (-mp, mp) which is partitioned into L intervals, each of magnitude 2mp/L. Now each sample is approximated or rounded off to the nearest quantized level as shown in the figure. Since each sample is now approximated to one of the L numbers therefore the information is digitized.
The quantized signal is an approximation of the original. We can improve the accuracy of the quantized signal to any desired degree simply by increasing the number of levels L.