Discrete Fourier Transform Interview Questions and Answers:
1. What is zero padding? What are its uses?
Ans. Let the sequence x(n) has a length L. If we want to find the N-point DFT (N > L) of the sequence x(n), we have to add (N — L) zeros to the sequence x(n). This is known as zero padding. The uses of padding a sequence with zeros are
- We can get “better display” of the frequency spectrum.
- With zero padding, the DFT can be used in linear filtering.
2. Define discrete Fourier series?
Ans. Consider a sequence xp(n) with a period of N samples so that xp(n) = xp(n + lN); Then discrete Fourier series of the sequence xp(n) is defined as
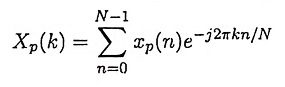
3. What do you understand by periodic convolution?
Ans. Let x1p(n) and x2p(n) be two periodic sequences each with period N with
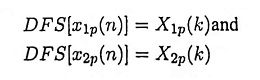
If
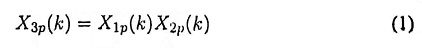
then the periodic sequence x3p(n) with Fourier series coefficients X3p(k) can be obtained by periodic convolution, defined as
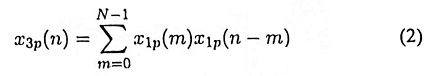
The convolution in the form of Eq. (2) is known as periodic convolution, as the sequences in Eq. (2) are all periodic with period N, and the summation is over one period.
4. Define circular convolution?
Ans. Let x1(n) and x2(n) are finite duration sequences both of length N with DFTs X1(k) and X2(k). If X3(k) = X1(k)X2(k), then the sequence x3(n) can be obtained by circular convolution, defined as
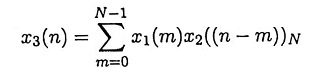
5. Distinguish between linear and circular convolution of two sequences
Ans.
| Sl no | Linear Convolution | Circular Convolution |
| 1 | If x(n) is a sequence of L Number of samples and h(n) with M number of samples, after convolution y(n) will contain N = L + M – 1 samples. | If x(n) is a sequence of L Number of samples and h(n) with M samples, after convolution y(n) will contain N = Max(L, M) samples. |
| 2 | Linear convolution can be used to find the response of a linear filter. | Circular convolution cannot be used to find the response of a linear filter. |
| 3 | Zero padding is not necessary to find the response of a linear filter. | Zero padding is necessary to find the response of a filter. |
6. How will you obtain linear convolution from circular convolution?
Ans. Consider two finite duration sequences x(n) and h(n) of duration L samples and M samples respectively. The linear convolution of these two sequences produces an output sequence of duration L + M — 1 samples, whereas, the circular convolution of x(n) and h(n) give N samples where N = Max(L, M). In order to obtain the number of samples in circular convolution equal to L + M — 1, both x(n) and h(n) must be appended with appropriate number of zero valued samples. In other words, by increasing the length of the sequences x(n) and h(n) to L + M — 1 points and then circularly convolving the resulting sequences we obtain the same results as that of linear convolution.
7. What is meant by sectioned convolution?
Ans. If the data sequence x(n) is of long duration, it is very difficult to obtain the output sequence y(n) due to limited memory of a digital computer. Therefore, the data sequence is divided up into smaller sections. These sections are processed separately one at a time combined later to get the output.
8. What are the two methods used for the sectional convolution?
Ans. The two methods used for the sectional convolution are (1) the overlap-add method and (2) overlap-save method.
9. Write briefly about overlap-save method?
Ans. In the method the data sequence is divided into N-point sections xi(n). Each section contains the last M —1 data points of the previous section followed by L new data points to form a data sequence of length N = L+ M —1. If we take N-point circular convolution of xi(n) with h(n), the first M – 1 points will not agree with the linear convolution of xi(n) and h(n) because of aliasing; the remaining (N — M + 1) points however will agree with the linear convolution. Hence we discard the first (M — 1) points of filter section xi(n) N h(n). This process is repeated for all sections and the filtered sections are abutted together.
10. Write briefly about overlap-add method?
Ans. In this method the size of the input data block xi(n) is L. To each data block we append M – 1 zeros and perform N-point (N = L+ M —1) circular convolution of xi(n) with h(n). Since each data block is terminated with M — 1 zeros, the last M —1 points from each output block must be overlapped and added to first M —1 points of the succeeding block. Hence, this method is called overlap-add method.
11. State the difference between (i) overlap-save method (ii) overlap-add method.
Ans.
| Sl no | Overlap-save method | Overlap-add method |
| 1 | In this method the size of the input data block is N = L + M -1. | In this method the size of the input data block is L. |
| 2 | Each data block consists of the last M -1 data points of the previous data block followed by L new data points. | Each data block is L points and we append M – 1 zeros to compute N-point DFT. |
| 3 | In each output block M – 1 points are corrupted due to aliasing, as circular convolution is employed. | In this no corruption due to aliasing, as linear convolution is performed using circular convolution. |
| 4 | To form the output sequence the first M – 1 data points are discarded in each output block and the remaining data are fitted together. | To form the output sequence, the last M -1 points from each output block is added to the first (m – 1) points of the succeeding block. |
12. Distinguish between DFT and DTFT.
Ans.
| Sl no | DFT | DTFT |
| 1 | Obtained by performing sampling operation in both the time and frequency domains. | Sampling is performed only in time domain |
| 2 | Discrete frequency spectrum. | Continuous function of ω |
13. Distinguish between Fourier series and Fourier transform.
Ans.
| Sl no | Fourier series | Fourier transform |
| 1 | Gives the harmonic content of a periodic time function. | Gives the frequency information for an aperiodic signal. |
| 2 | Discrete frequency spectrum. | Continuous frequency spectrum |