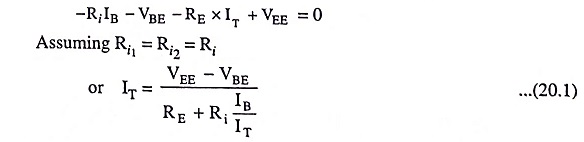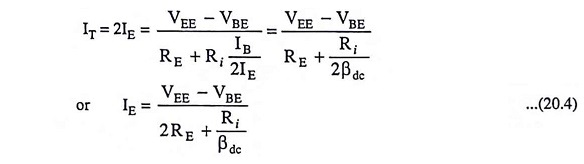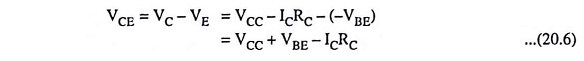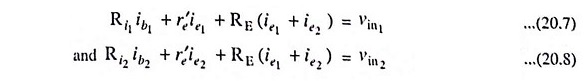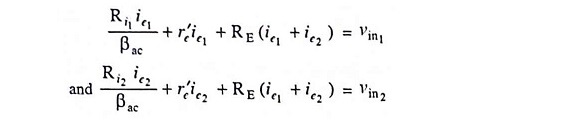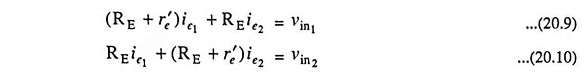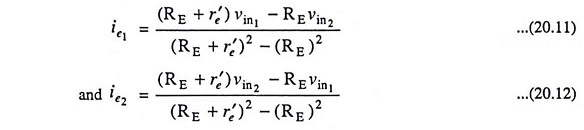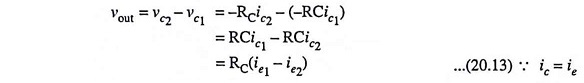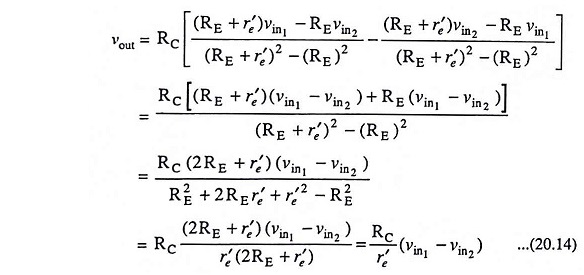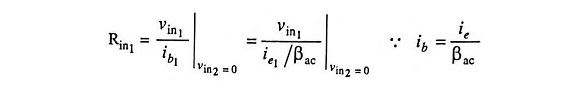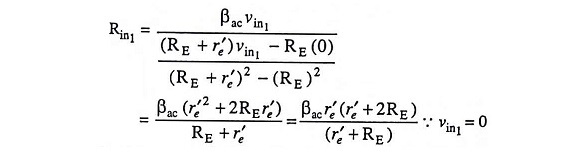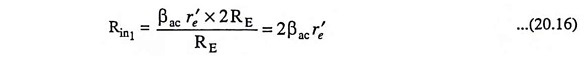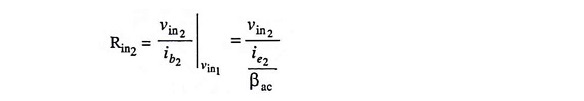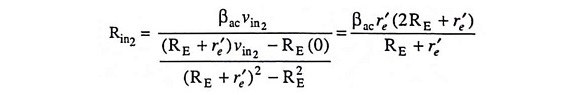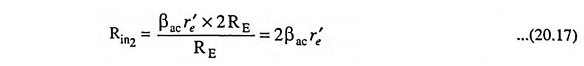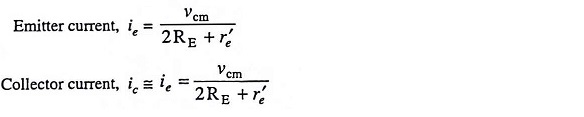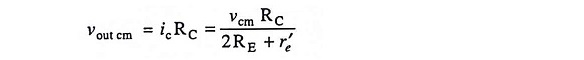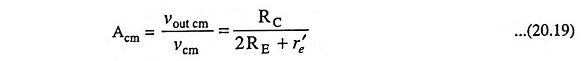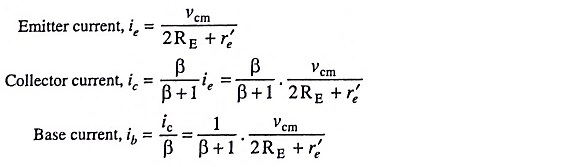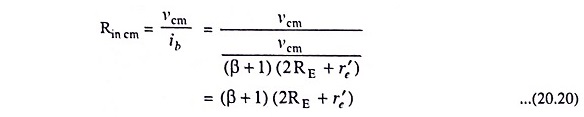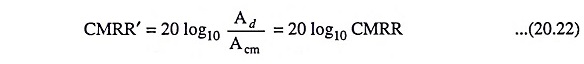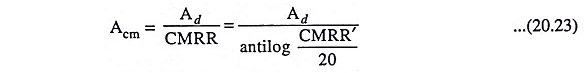Dual Input Balanced Output Differential Amplifier:

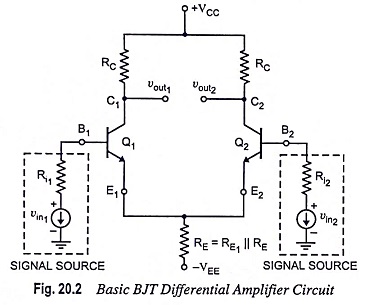
The dual input balanced output differential amplifier configu­ration is shown in Fig. 20.2. In the given circuit two input signals v_in1 and v_in2 are applied to the bases B₁ and B₂ of transistors Q₁ and Q₂. The differential input under amplification is the differ­ence of the two input signals v_in1 and v_in2 and denoted by v_d. The output in this configuration is balanced as it is measured between the two collectors C₁ and C₂, which are at the same dc potential w.r.t. ground.

1. DC Analysis:

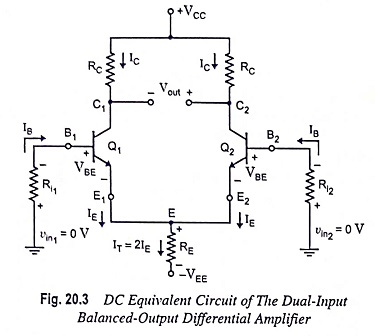
DC analysis of a differential amplifier circuit is done for determination of operating points (I_CQ and V_CEQ) when no signal is applied (i.e., v_in1 = v_in2 = 0). For dc analysis we require a dc equivalent circuit of the differential amplifier. The dc equivalent circuit of the circuit given in Fig. 20.2 is shown in Fig. 20.3 which is obtained by setting v_in1 = v_in2 = 0. Since, both the transistors Q₁ and Q₂ are identical (matched pair) and also the passive loads (R_C1 = R_C2 = R_C) are the same, we are to determine Q-point for transistor Q₁ only. The same Q-point can be used for transistor Q₂ also.

Applying Kirchhoff’s voltage law to the base-emitter loop of the transistor Q₁ [Fig. 20.3].

and base current,

Applying Kirchhoff’s current law at node E, we have

Substituting I_T = 2I_E from Eq. (20.3) and I_B = I_E/β_dc  from Eq.(20.2) in Eq. (20.1), we have

where V_BE = 0.7 V for silicon transistors and V_BE = 0.3 V for germanium transistors.

Usually, R_i/β_dc << 2R_E and , therefore, Eq. (20.4) can be rewritten as

From above Eq. (20.5), we see that the value of R_E fixes the emitter current in transistors Q₁ and Q₂ for a given value of –V_EE. Thus, the desired value of the emitter dc bias current for a given value of –V_EE can be obtained by selecting emitter resistance R_E of a proper value. Thus, we see that emitter current in transistors Q₁ and Q₂ is independent of collector resistance R_C.

The voltage at the emitter of transistor Q₁ is approximately equal to –V_BE if the voltage drop across R_i is assumed to be negligibly small. Knowing the value of emitter current I_E from Eq. (20.5), the voltage at the collector, V_C can be determined from the following equation

and collector-to-emitter voltage,

Hence for both transistors I_CQ and V_CEQ can be determined by using Eqs. (20.4) and (20.6) respectively, because at the Q-point, I_E = I_CQ and V_CE = V_CEQ.

The noteworthy point is that the dc analysis Eqs. (20.4) and (20.6) are applicable to all four differential amplifier configurations as long as the biasing arrangement (as discussed above) is the same for each of them.

2. AC Analysis:

The expressions for the differential voltage gain A_d, common mode gain A_cm and the input resistance R_in can be derived from ac analysis of the dual input balanced output differential amplifier.

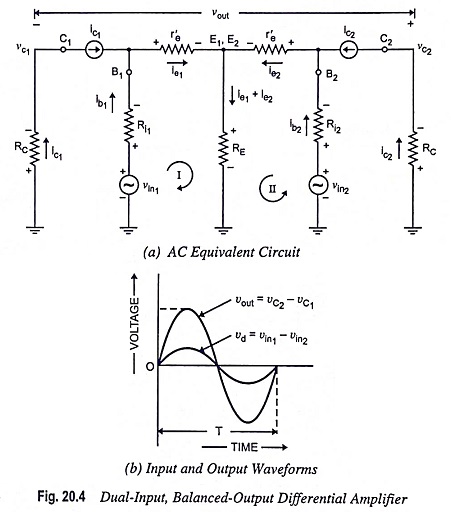
For ac analysis of the differential amplifier shown in Fig. 20.2, the dc voltages +V_CC and –V_EE are set at zero and small signal T-equivalent models are substituted for the transistors Q₁ and Q₂, as shown in Fig. 20.4 (a).

The noteworthy points about the circuit given in Fig. 20.4(a) are as follows:

1. Emitter currents I_E1 and I_E2 are equal, so r′_e1 = r′_e2. That is why, the dynamic or ac emitter resistance of transistors Q₁ and Q₂ is simply denoted by r′_e.
2. The voltage across each collector resistor is shown to have a phase difference of 180° (i.e., in phase opposition) with respect to input voltages v_in1 and v_in2. The polarity assignment is according to the CE configuration, the differential amplifier being basically constructed in CE configuration using two identical CE circuits.
3. The polarity of the output voltage v_out indicates that the voltage at collector C₂ is assumed to be more positive with respect to that of collector C₁, even though both of them are negative w.r.t. ground.

(i) Voltage Gain: Applying KVL to loops I and II of the circuit given in Fig. 20.4 (a), we have

Substituting i_b1 = i_e1/β_ac and i_b2 = i_e2/β_ac in above equations, we have

Usually R_i1/β_ac and R_i2/β_ac, being very small, are neglected and, therefore, the above equations become as follows:

Solving above Eqs. (20.9) and (20.10) for currents i_e1 and i_e2, we have

The output voltage is given by

Substituting the values of i_e1 and i_e2 from Eqs. (20.11) and (20.12) in above equation, we have

Above Eq. (20.14) shows that a differential amplifier amplifies the difference of two input signals as expected. The input and output waveforms of the dual input balanced output differential amplifier are depicted in Fig. 20.4 (b).

By defining v_in1 – v_in2 = v_d as the difference in input voltages, the voltage gain equation for the dual input balanced output differential amplifier is given by

Above Eq. (20.15) reveals that the voltage-gain equation for the differential amplifier is independent of emitter resistance R_E and this equation is identical to the voltage-gain equation of the CE amplifier.

(ii) Differential Input Resistance: Differential input resistance seen from the signal source is defined as the equivalent resistance that would be measured at either input terminals with the other terminal grounded. Usually source resistances R_i1 and R_i2 are negligibly small and, therefore, will be ignored in the derivation of input resistances R_in1 and R_in2 seen seen from the input signal sources v_in1 and v_in2 respectively.

The input resistance R_in1 seen from the input signal source v_in1 is determined by setting signal source v_in2 at zero and is expressed in equation form as

Substituting the value of i_e1 from Eq. (20.11) in above equation, we have

Usually, R_E >> r’_e which implies that (r′_e + 2R_E) ≡ 2R_E and (r′_e + R_E) ≡ R_E and, therefore, above equation becomes

Similarly, the input resistance R_in2 seen from the input signal v_in2 is determined with the signal source v_in1 set at zero and is expressed in equation form as

Substituting the value of i_e2 from Eq. (20.12) in above equation, we have

However, (2R_E + r′) ≡ 2R_E and (R_E + r_e) = R_E since r′_e << R_E and, therefore, the above equation for R_in2 becomes as

(iii) Output Resistance: The output resistance may be defined as the equivalent resistance measured at either output terminal with respect to ground. Hence, the output resistance R_out1 measured between collector C₁ and ground is equal to collector resistance R_C [Fig. 20.4 (a)] i.e., R_out1 = R_C.

Similarly, the output resistance R_out2 measured between collector C₂ and ground is equal to collector resistance R_C i.e., R_out1 = R_C.

3. Noninverting and Inverting Inputs:

In the differential amplifier circuit shown in Fig. 20.2, the input voltage v_in1 is referred to as a noninverting input as a positive voltage v_in1 acting alone provides a positive output voltage. This is obvious from voltage-gain Eq. (20.14). Similarly, the positive voltage v_in2 acting alone produces a negative output voltage, and therefore, v_in2 is referred to as a inverting input [Eq. (20.14)]. Consequently, the base terminal B₁ to which v_in1 is impressed is known as the noninverting input terminal, and the base terminal to which v_in2 is applied is known as the inverting input terminal. Noninverting input terminal is marked with plus (+) sign and inverting input terminal is marked with minus (-) sign.

4. Common-Mode Voltage Gain:

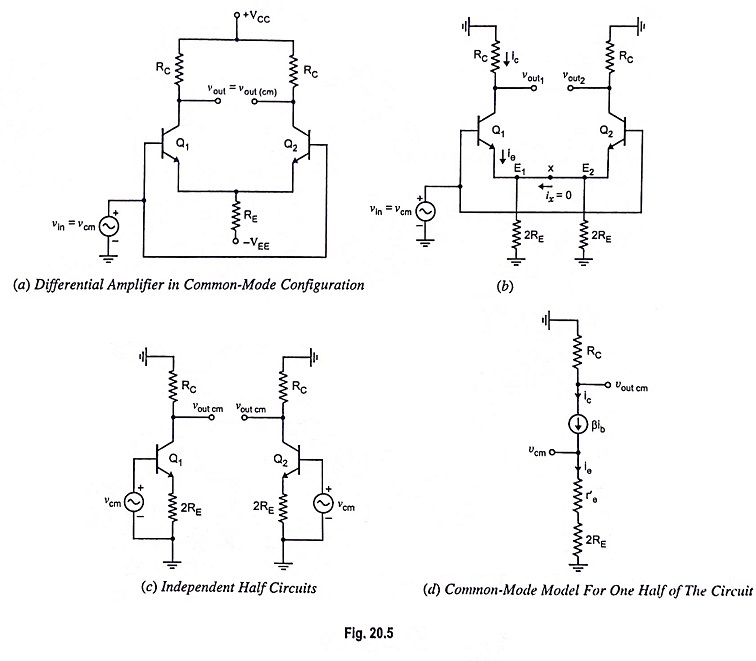
If in-phase signals v_in are applied to each base of the differential amplifier, as depicted in Fig. 20.5(a), the input signal is referred to as common-mode signal v_cm. Ideally, there will be no ac output voltage with a common-mode input signal because the voltage between the bases is zero. However, due to imperfections within the differential amplifier there will be a small ac output voltage.

In Fig. 20.5(a) equal voltages are applied to the two inputs. A differential amplifier is never used deliberately in this way because the output voltage would be ideally zero. Then what is the need of discussing such a circuit. This is because most static, interference, and other kinds of undesirable pickups are common mode signals.

Because the differential amplifier is a symmetrical circuit, emitter resistance R_E can be split into two parallel resistors, as illustrated in Fig. 20.5 (b). Because of symmetry of the circuit, lead connecting the two emitters E₁ and E₂ carries no current i.e., i_x = 0 because emitters E₁ and E₂ are at the same potential.

With i_x = 0, connection between two emitters can be eliminated and the resulting independent half circuits are shown in Fig. 20.5 (c). The common-mode behavior can be determined from only one-half of the circuit.

Using r-parameters, the common model for one half of the circuit is depicted in Fig. 20.5 (d).

Referring to Fig. 20.5 (d), we have

The common-mode output voltage is, therefore,

The common-mode voltage gain A_cm is, therefore,

5. Common-Mode Input Resistance R_{in cm}

Common-mode input resistance is obtained as under:

Common mode input resistance,

6. Common-Mode Rejection Ratio (CMRR)

Having defined differential voltage gain A_d and common mode voltage gain A_cm, a value of the common-mode rejection ratio (CMRR) can be calculated from the following equation

i.e., CMRR may be defined as the ratio of differential voltage gain to common-mode voltage gain.

If a differential amplifier is perfect, CMRR would be infinite because in that case common-mode voltage gain A_cm would be zero.

The value of CMRR can also be expressed in logarithmic terms as

Data sheets usually list the values of A_d and CMRR’, but not the value of A_cm. However, the value of A_cm can be determined from the following equation