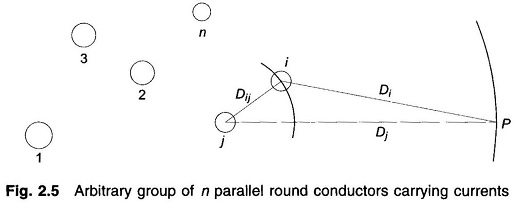
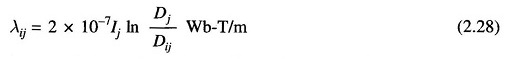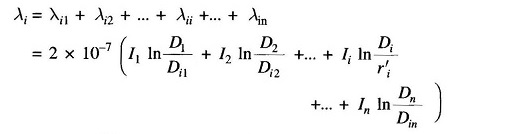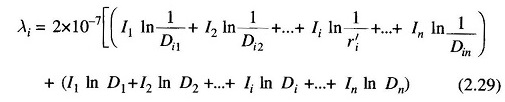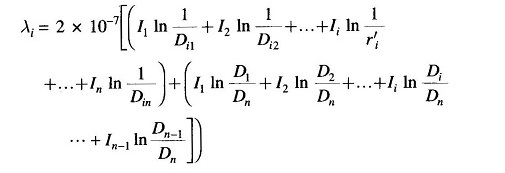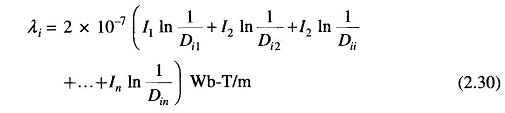Flux Linkage of n Parallel Conductors Carrying Current:

As shown in Fig. 2.5, consider a group of n parallel conductors carrying current I₁, I₂ ,…, I_n whose sum equals zero. Distances of these conductors from a remote point P are indicated as D₁, D₂ ,…, D_n. Let us obtain an expression for the total Flux Linkages of the ith conductor of the group considering flux up to the point P only.

The flux linkages of ith conductor due to its own current I_i (self linkages) are given by

The Flux Linkage of conductor i due to current in conductor j is

where D_ij is the distance of ith conductor from jth conductor carrying current I_j. From Eq. (2.27) and by repeated use of Eq. (2.28), the total flux linkages of parallel conductors carrying current i due to flux up to point P are

The above equation can be reorganized as

But,

Substituting for I_n in the second term of Eq. (2.29) and simplifying, we have

In order to account for total flux linkages of conductor i, let the point P now recede to infinity. The terms such as In D₁/D_n, etc. approach In 1 = 0. Also for the sake of symmetry, denoting r′_i as D_ii, we have