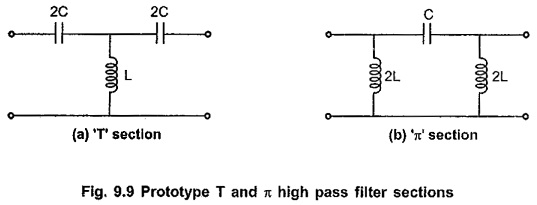
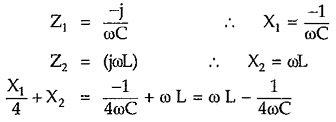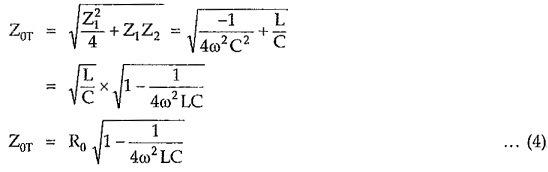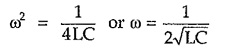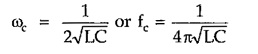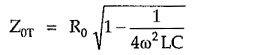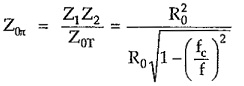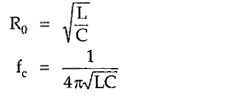High Pass Filter:

The prototype high pass filter T and π sections are as shown in the Fig. 9.9.

Design Impedance (R₀):

Total series arm impedance Z₁ = -j/ωC

Total shunt arm impedance Z₂ = jωL

Hence, Z₁ . Z₂ =(-j/ωC) (jωL) = L/C which is real and constant. Hence above sections are constant K sections. So we can write,

Reactance Curves and Expression for Cut-off Frequency:

As both T and π sections have same cut-off frequency, it is sufficient to calculate the cut-off frequency for the T section only.

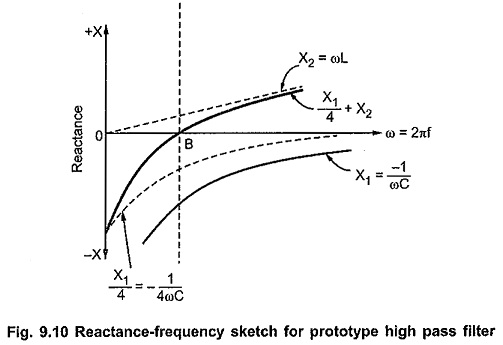
The reactance curves are as shown in the Fig. 9.10.

From above characteristics it is clear that all the reactance curves have positive slope as all curves slope upward to the right side with increasing ω.

Here the curves are on the same side of the horizontal axis up to the point B, giving a stop band. For frequencies above point B, the curves are on opposite sides of the axis, giving pass band. Thus, point B gives cut-off frequency, represented as ω = ω_c.

At point B, ω = ω_c, the curve for (X₁/4 + X₂) crosses the frequency axis, hence we can write,

The algebraic approach to calculate cut-off frequency is as follows.

From above expression it is clear that, Z_0T is real if 1/4ω²LC < 1 and imaginary if 1/4ω²LC > 1. Hence condition 1 – 1/4ω²LC = 0 gives expression,

Thus, above prototype section passes all frequencies above ω = 1/2√LC while attenuates all frequencies below this value. Therefore cut-off frequency of high pass filter is given by

Above frequency comes out to be same as frequency calculated by reactance sketch method.

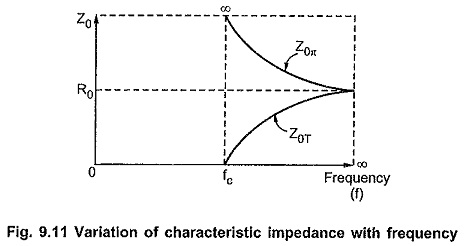
Variation of Z_0T and Z_0π with Frequency:

Consider expression for Z_0T as

From equation (2) we can write,

Similarly we can write,

Hence,

From equation (5), it is clear that as frequency f increases from f_c to ∞ in pass band, Z_0T also increases from 0 to R₀. For π section, from equation (6), it is clear that as frequency increases from f_c to ∞, Z₀ decreases from ∞ to R₀ in pass band. The variation of Z_0T and Z_0π with frequency is as shown in Fig. 9.11.

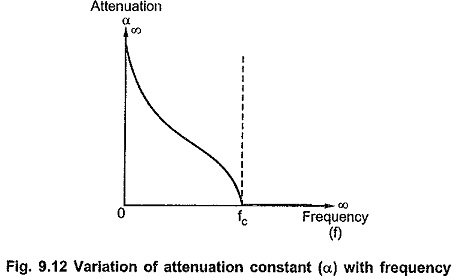
Variation of Attenuation Constant (α) with Frequency:

In pass band, attenuation is zero (α = 0). In stop band attenuation is given by

In stop band, as frequency f increases from 0 to f_c, attenuation decreases from ∞ to 0. The variation of attenuation constant α with frequency is as shown in the Fig. 9.12.

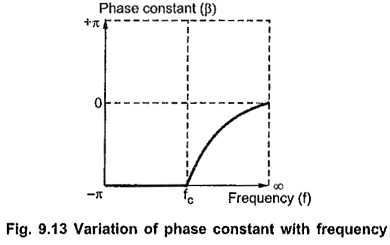
Variation of Phase Constant β with Frequency:

In stop band, phase constant β is always π radian. In pass band where α = 0, the phase angle β is given by

From the above equation it is clear that in pass band when frequency f increases from f_c to ∞, β decreases to 0. The variation of phase constant β with frequency is as shown in the Fig. 9.13.

Design Equations of Prototype High Pass Filter:

The design impedance R₀ and cut-off frequency f_c for high pass filter section can be given in terms of L and C as follows

Dividing equation for R₀ by f_c, we get,

Multiplying equation for R₀ and f_c, we get,

Equation (9) and (10) are called design equations of prototype high pass filter sections.