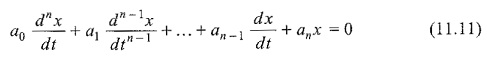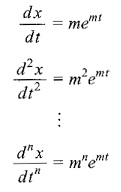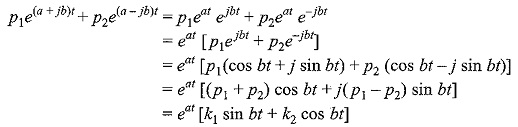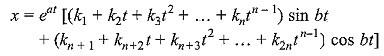Homogeneous Linear Differential Equations:

Consider an nth order homogeneous linear differential equations with constant coefficients,

where a₀, a₁ … a_n are real constants.

Now we shall find the solution of Eq. 11.11 of the form x = e^mt. By assuming that x = e^mt is a solution for certain m, we have

Substituting in Eq. 11.11, we get

or

where

This is called the auxiliary, or the characteristic equation of the given Homogeneous Linear Differential Equations. Three cases might occur in the auxiliary equation which are, subject to the roots of Eq. 11.12 being real and distinct, real and repeated, or complex.

Case 1 Distinct real roots:

If the roots of the Eq. 11.12, m₁, m₂ … m_n are real and distinct, the general solution of Eq. I 1.11 is

where k₁, k₂ … k_n are arbitrary constants.

k₁, k₂ … k_n values can be determined by using initial conditions.

Case 2 Roots are real and repeated:

If the roots of Eq. 11.12 are the double real root m, and (n -2) distinct real roots.

then the linearly independent solutions of Eq. 11.11 are

And the general solution may be written as

Similarly, if Eq. 11.12 has a triple real root m, the general solution is (c₁ + c₂t + c₃t²) e^mt.

Case 3 Roots are Complex Conjugate:

Consider the auxiliary equation which has the complex number a + jb as a non-repeated root. The corresponding part of the general solution is p₁e^(a+jb)t + p₂e^(a-jb)t, where p₁ and p₂ are arbitrary constants.

where

are the new arbitrary constants.

If however, (a + jb) and (a — jb) are each n roots of the auxiliary equation, the corresponding general solution may be written as