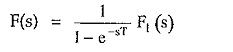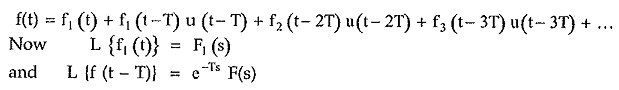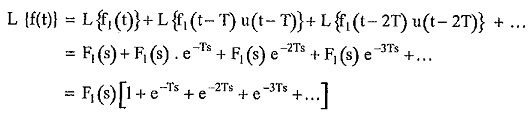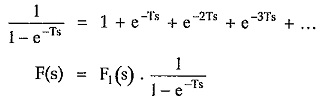Laplace Transform of Periodic Function:

Consider a Laplace Transform of Periodic Function of time period T satisfying the condition,

where n is positive or negative integer.

The Laplace transform of such periodic function is given by ,

where F₁ (s) is the Laplace transform of the first cycle of the periodic function.

Proof:

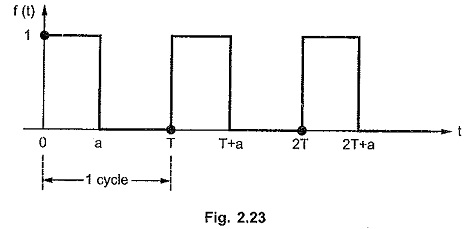
Consider the periodic function f(t) shown in the Fig. 2.23.

Let f₁ (t) be the first cycle of periodic function f(t). It can be expressed interms of unit step function as,

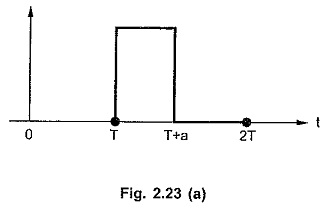
Consider the second cycle of the function f(t) as shown in the Fig. 2.23 (a).

This can be expressed as,

It can be seen from the expression of f₁ (t) that,

Multiplication by u(t – T) confirms that f₂ (t) i.e. second cycle is zero for t < T.

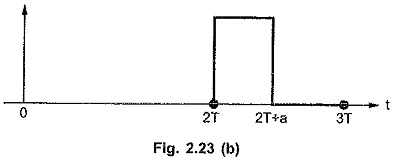
Consider the third cycle as shown in the Fig. 2.23 (b).

This can be expressed as,

It can be seen from the expression of f₁ (t) that,

Multiplication u (t – 2T) confirms that f₃ (t) i.e. second cycle is zero for t < 2T.

From equations (1), (2) and (3) we can write the expressions for various cycles as,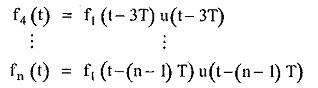

Hence the given function f(t) can be written as,

by shifting property

Hence we can write Laplace transform of f(t) as,

Now

where F₁(s) is the Laplace transform of first cycle of periodic function f(t).