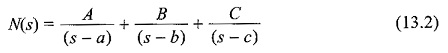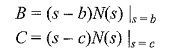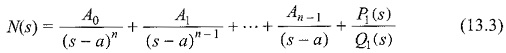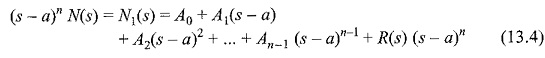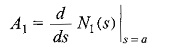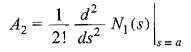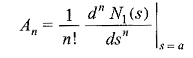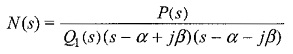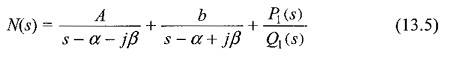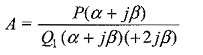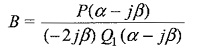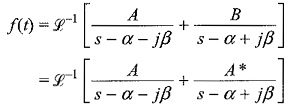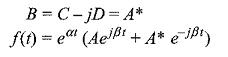Laplace Transform Partial Fraction:
Most transform methods depend on the partial fraction of a given transform function. Given any solution of the form N(s) = P(s)/Q(s), the inverse Laplace transform can be determined by expanding it into partial fractions. The Laplace Transform Partial Fraction depend on the type of factor. It is to be assumed that P(s) and Q(s) have real coefficients and contain no common factors. The degree of P(s) is lower than that of Q(s).
Case 1:
When roots are real and simple
In this case
N(s) = P(s)/Q(s)
where
Q(s) = (s – a)(s – b)(s – c)
Expanding N(s) into partial fractions, we get
To obtain the constant A, multiplying Eq. 13.2 with (s — a) and putting s = a, we get
Similarly, we can get the other constants
Case 2:
When roots are real and multiple
In this case
N(s) = P(s)/ Q(s)
where
Q(s) = (s – a)n Q1(s)
The partial fraction expansion of N(s) is
where P1(s)/Q1(s) = R(s) represents the remainder twins of expansion. To obtain the constant A0,A1,…, An-1, let us multiply both sides of Eq. 13.3 by (s – a)n
Thus
where R(s) indicates the remainder terms.
Putting s = a, we get
Differentiating Eq. 13.4 with respect to s, and putting s = a, we get
Similarly,
In general,
Case 3:
When roots are complex
Consider a function
The partial fraction expansion of N(s) is
where P1(s)/Q1(s) is the remainder term.
Multiplying Eq. 13.5 by (s – α – jβ) and putting s = α + jβ, we get
Similarly,
In general, B = A* where A* is complex conjugate of A.
If we denote the inverse transform of the complex conjugate terms as f(t)
where A and A* are conjugate terms.
If we denote A = C + jD, then