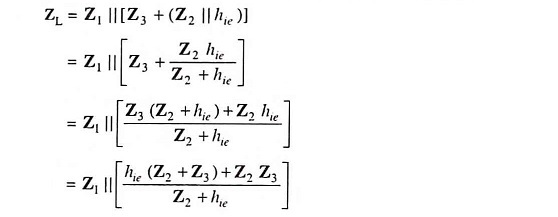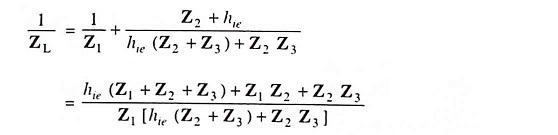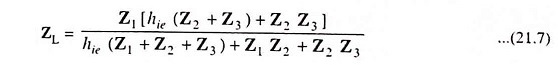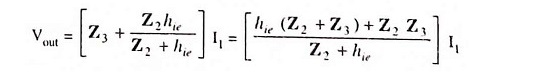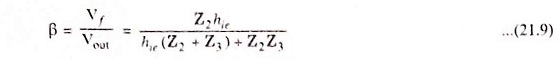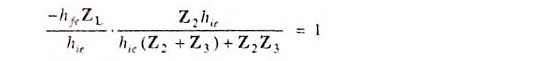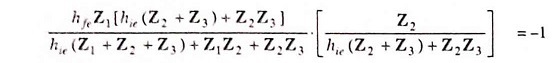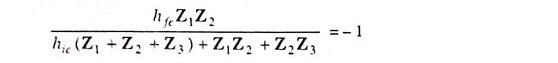LC Oscillator Circuit – Definition, Types and Equation:

Oscillators, which use inductance-capacitance (L-C) circuits as their tank or oscillatory circuits are called LC Oscillator. LC Oscillator are very popular for generating high-frequency outputs (e.g. 10 kHz to 100 MHz). There is a large variety of LC Oscillators such as tuned collector oscillators, tuned base oscillators, Colpitt’s oscillators, Hartley oscillators, Clapp oscillators, crystal oscillators etc.

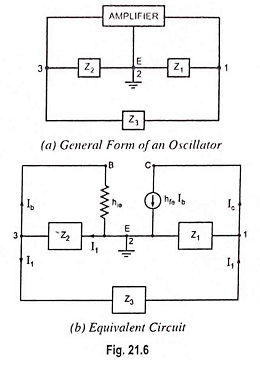
General form of an L-C Oscillator:

In the general form of an oscillator depicted in Fig. 21.6 (a), any of the active devices such as vacuum tube, BJT, FET or op-amp may be used in the amplifier section, Z₁, Z₂ and Z₃ are the reactive elements constituting the feedback tank circuit which determines the frequency of oscillation. Here, Z₁ and Z₂ serve as an ac voltage divider for the output voltage and feedback signal. Thus, the voltage across Z₂ is the feedback signal. The equivalent circuit is drawn in Fig. 21.6 (b) with the following two assumptions:

1. h_re of transistor is negligibly small and, therefore, the feedback source h_reV_out is negligible.
2. h_oe of the transistor is very small i.e. the output resistance 1/h_oe is very large and, therefore, 1/h_oe is omitted from equivalent circuit.

Let us determine the load impedance between output terminals 1 and 2. Here Z₂ and h_ie are in parallel and their resultant impedance is in series with impedance Z₃.

The equivalent impedance is in parallel with impedance Z₁. Thus load impedance between output terminals is given as

or

or

The voltage gain of a CE amplifier without feedback is given as

The output voltage between terminals 1 and 2 is given as

The voltage feedback to the input terminals 2 and 3 is given as

So feedback fraction,

Applying the criterion of oscillation i.e. Aβ = 1, we have

Substituting the value of Z_L from Eq. (21.7). we have

or

or

or

or

This is the general equation for the LC Oscillator Circuit.