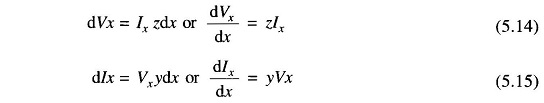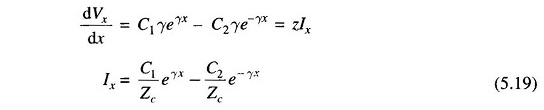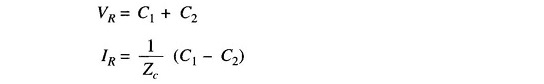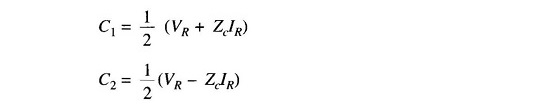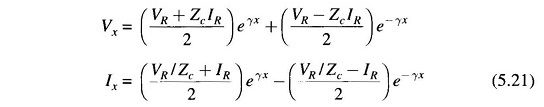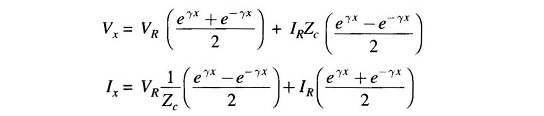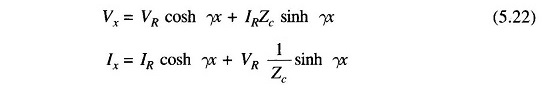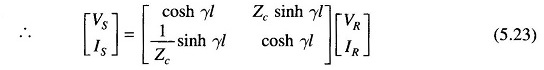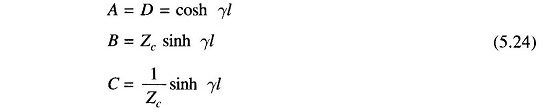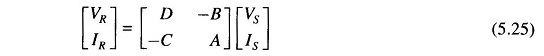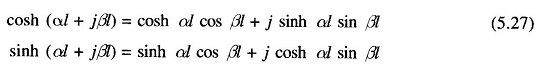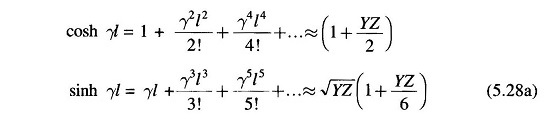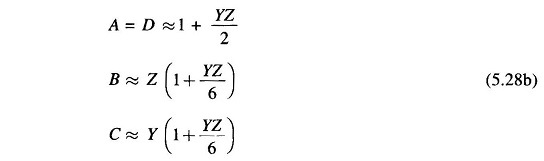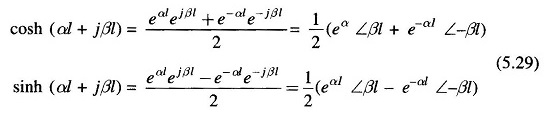Long Transmission Line:

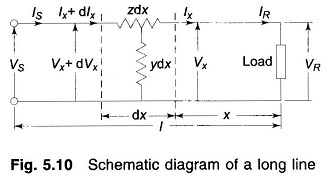
For lines over 250 km, the fact that the parameters of a line are not lumped but distributed uniformly throughout its length, must be considered. Figure 5.10 shows one phase and the neutral return (of zero impedance) of a Long Transmission Line.

Let dx be an elemental section of the line at a distance x from the receiving-end having a series impedance zdx and a shunt admittance ydx. The rise in voltage to neutral over the elemental section in the direction of increasing x is dV_x. We can write the following differential relationships across the elemental section:

It may be noticed that the kind of connection (e.g. T or π) assumed for the elemental section, does not affect these first order differential relations. Differentiating Eq. (5.14) with respect to x, we obtain

Substituting the value of dI_x/dx from Eq. (5.15), we get

This is a linear differential equation whose general solution can be written as follows:

where

and C₁ and C₂ are arbitrary constants to be evaluated.

Differentiating Eq. (5.17) with respect to x:

Where

The constants C₁ and C₂ may be evaluated by using the end conditions, i.e. when x = 0, V_x = V_R and I_x = I_R. Substituting these values in Eqs. (5.17) and (5.19) gives

which upon solving yield

With C₁ and C₂ as determined above, Eqs. (5.17) and (5.19) yield the solution for V_x and I_x as

Here Z_c is called the characteristic impedance of the Long Transmission Line and γ is called the propagation constant.

Knowing V_R, I_R and the parameters of the line, using Eq. (5.21) complex number rms values of V_x and I_x at any distance x along the line can be easily found out.

A more convenient form of expression for voltage and current is obtained by introducing hyperbolic functions. Rearranging Eq. (5.21), we get

These can be rewritten after introducing hyperbolic functions, as

where x = l, V_x = V_s, I_x = I_s

Here

In case [V_S I_S] is known, [V_R I_R] can be easily found by inverting Eq. (5.23).

Thus

Evaluation of ABCD Constants:

The ABCD constants of a long Long Transmission Line can be evaluated from the results given in Eq. (5.24). It must be noted that γ=√yz is in general a complex number and can be expressed as

The hyperbolic function of complex numbers involved in evaluating ABCD constants can be computed by any one of the three methods given below.

Method 1:

Note that sinh, cosh, sin and cos of real numbers as in Eq. (5.27) can be looked up in standard tables.

Method 2:

This series converges rapidly for values of γl usually encountered for power lines and can be conveniently approximated as above. The corresponding expressions for ABCD constants are

The above approximation is computationally convenient and quite accurate for lines up to 400/500 km.

Method 3: