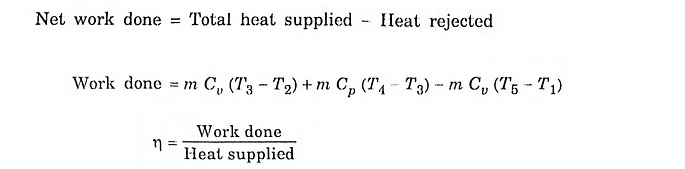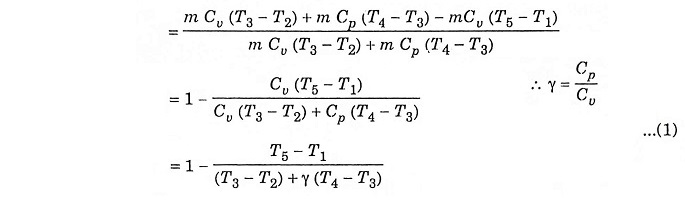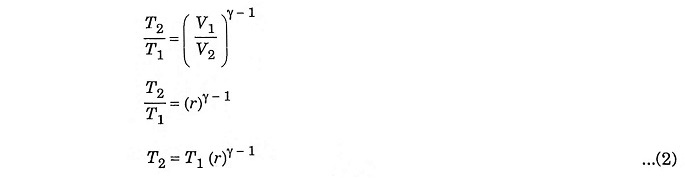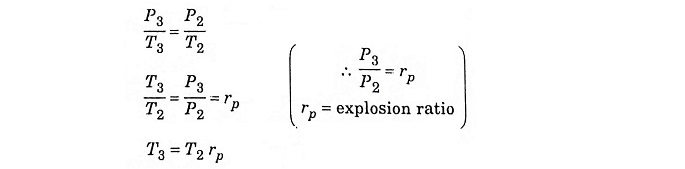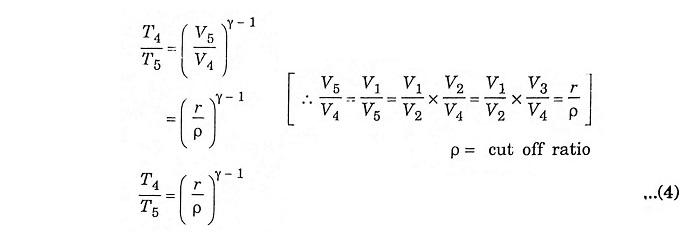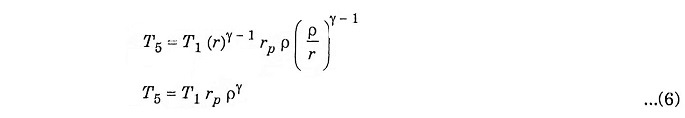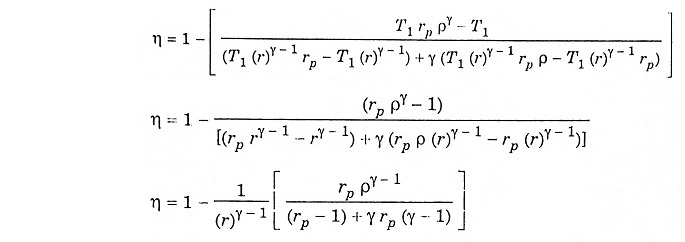Mixed/Dual Cycle – Process and its Derivation:
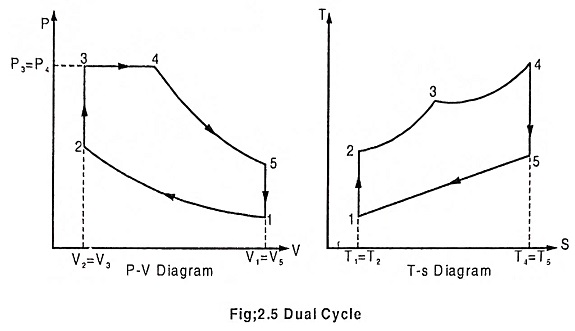
Mixed/Dual cycle is a combination of Otto cycle and Diesel cycle, where heat addition takes place partly at constant volume and partly at constant pressure. In fact Otto cycle and Diesel cycle are special cases of Dual cycle. Both Otto cycle (constant volume heat addition) and Diesel cycle (constant pressure heat addition) are over simplistic and unrealistic. In actual case, combustion takes place neither at constant volume (time required for chemical reaction), nor at constant pressure (rapid uncontrolled combustion). Dual cycle is used to model the combustion process and consists of the following operation.
Process 1 – 2 – Adiabatic compression
In this process, the piston moves from BDC to TDC, the air or air-fuel mixture undergoes adiabatic compression. The volume decreases from V1 to V2, pressure rises from P1 to P2, temperature rises from T1 to T2 and the entropy remains constant (isentropic process) S1 = S2.
Process 2 – 3 – Addition of heat at constant volume
The piston remains at the TDC for a moment, it is the time required for chemical reaction. Heat is added at constant volume V2 = V3. Pressure increases from P2 to P3. Temperature increases from T2 to T3, entropy increases from S2 to S3.
Process 3 – 4 – Addition of heat at constant pressure
The piston remains at the TDC position, heat is added at constant pressure P3 = P4, the volume increases from V3 to V4. The temperature increases from T3 to T4 and the entropy also increases from S3 to S4.
Process 4 – 5 – Adiabatic expansion
The piston moves from TDC to BDC position. Due to the combustion the mixture undergoes adiabatic expansion, the volume increases from V4 to V5, pressure decreases from P4 to P5, temperature decreases from T4 to T5 and the entropy remains same (isentropic process) S4 = S5.
Process 5 – 1 – Heat rejection at constant volume
The piston remains at the BDC position for a moment. Heat is rejected at constant volume. V5 = V1. The pressure decreases from P5 to P1 and temperature decreases from T5 to T1. Entropy also decreases from S5 to S1.
Air standard efficiency:
Compression ratio
In process 1 – 2, adiabatic compression,
In process 2 – 3 constant volume heating
Substituting T2 from equation (2)
In the process 4 – 5 – adiabatic expansion
In constant pressure heating process
Substituting the value of T3 from equation (3)
Substituting the value of T4 from equation (5) to equation (4) we get
Substituting the value of T2, T3, T4 and T5 in equation (1) we get