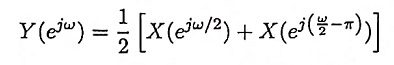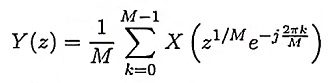Multirate Digital Signal Processing Interview Questions and Answers:
1. What is multirate signal processing?
Ans. The theory of processing signals at different sampling rates is called multirate signal processing.
2. Define down sampling
Ans. Down sampling a sequence x(n) by a factor M is the process of picking every Mth sample and discarding the rest.
3. What is mean by upsampling?
Ans. Upsampling by a factor L is the process of inserting i – 1 zeros between two consecutive samples.
4. If the spectrum of a sequence x(n) is X(ejω), then what is the spectrum of a signal down sampled by a factor 2
Ans.
5. If the z-transform of a sequence x(n) is X(z) then What is the z-transform of a sequence down sampled by a factor M?
Ans.
6. If the z-transform of a sequence x(n) is X(z) then what is the z-transform of a sequence upsampled by a factor L
Ans.
7. What is the need for anti-aliasing filter prior to down sampling?
Ans. The spectra obtained after down sampling a signal by a factor M is the sum of all the uniformly shifted and stretched version of original spectrum scaled by a factor 1/M. If the original spectrum is not band limited to π/M, then down sampling will cause aliasing. In order to avoid aliasing the signal x(n) is to be band limited to ± π/M. This can be done by filtering the signal x(n) with a lowpass filter with a cutoff frequency of π/M. This filter is known as anti-aliasing filter.
8. What is the need for anti-imaging filter after upsampling a signal?
Ans. The frequency spectrum of upsampled signal with a factor L, contains (L – 1) additional images of the input spectrum. Since we are not interested in image spectra, a lowpass filter with a cutoff frequency ωc = π/L can be used after upsampler. This filter is known as anti-imaging filter.