Unit Step Function | Unit Ramp Function | Unit Impulse Function | Unit Doublet Function: a) Unit step function: This function has already been discussed in the preceding It is defined as one that has magnitude of one for time greater … (Read More)

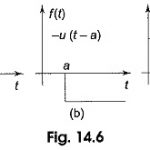
Gate Function in Network Function: By the use of step functions, any pulse of unit height can be realized. The pulse of width a can be generated by combining unit step function u(t) and delayed … (Read More)

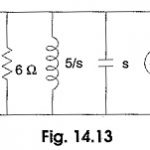
Transfer Function of Two Port Network: For a one-port network, the driving point impedance or impedance of the network is defined as The reciprocal of the impedance function is the driving point admittance function, and is denoted by Y(s). For the Transfer Function … (Read More)

Poles and Zeros of Transfer Function: Poles and Zeros of Transfer Function defines that, in general, the network function N(s) may be written as where a0,a1,…a2 and b0,b1,…bm are the coefficients of the polynomials P(s) and Q(s); they are real and positive for a … (Read More)

Conditions For Driving Point Function: The restrictions on pole and zero locations in the Conditions For Driving Point Function with common factors in P(s) and Q(s) cancelled are listed below. 1. The coefficients in the polynomials P(s) and Q(s) of network function … (Read More)

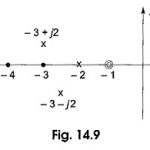
Poles and Zeros of Time Domain Response: For the given network function, a pole zero plot can be drawn which gives useful information regarding the critical frequencies. The Poles and Zeros of Time Domain Response can also be obtained from pole … (Read More)

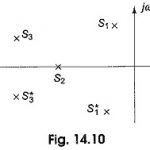
Stability Criterion in Network Function: Passive networks are said to be stable only when all the poles lie in the left half of the s-plane. Active networks (containing controlled sources) are not always stable. Consider transformed active network … (Read More)

Routh Criterion: The locations of the poles gives us an idea about stability of the active network. Consider the denominator polynomial To get a stable system, all the roots must have negative real parts. There should not be any … (Read More)