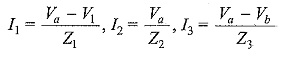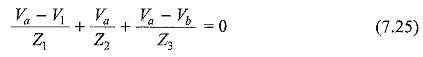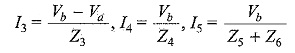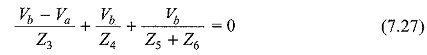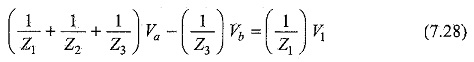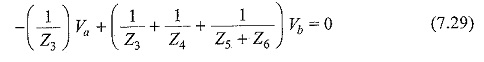Node Voltage Method:
The node voltage method can also be used with networks containing complex impedances and excited by sinusoidal voltage sources. In general, in an N node network, we can choose any node as the reference or datum node In many circuits, this reference is most conveniently chosen as the common terminal or ground terminal. Then it is possible to write (N – 1) nodal equations using KCL. We shall illustrate nodal analysis with the following example.
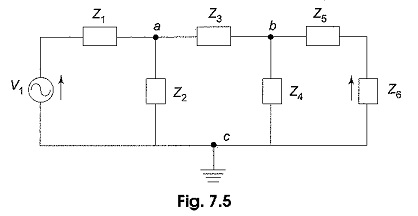
Consider the circuit shown in Fig.7.5.
Let us take a and b as nodes, and c as reference node. Va is the voltage between nodes a and c. Vb is the voltage between nodes b and c. Applying Kirchhoff’s current law at each node, the unknowns Va and Vb are obtained.
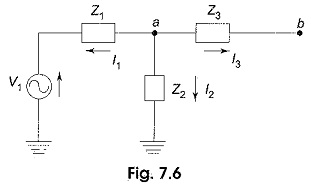
In Fig. 7.6, node a is redrawn with all its branches, assuming that all currents are leaving the node a.
In Fig. 7.6, the sum of the currents leaving node a is zero.
where
Substituting I1,I2 and I3 in Eq. 1, we get
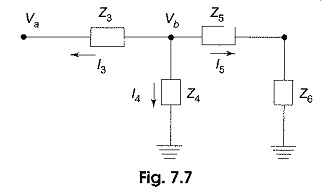
Similarly, in Fig. 7.7, node b is redrawn with all its branches, assuming that all currents are leaving the node b.
In Fig. 7.7, the sum of the currents leaving the node b is zero.
where
Substituting I3,I4 and I5 in Eq. 7.26
Rearranging Eqs 7.25 and 7.27, we get
From Eqs 7.28 and 7.29, we can find the unknown voltages Va and Vb.