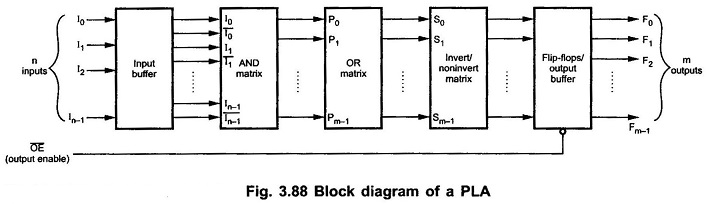
Programmable Logic Array (PLA) | Block Diagram of PLA:

The combinational circuit do not use all the minterms every time. Occasionally, they have don’t care conditions. Don’t care condition when implemented with a ROM becomes an address input that will never occur. The result is that not all the bit patterns available in the ROM are used, which may be considered a waste of available equipment. For cases where the number of don’t care conditions is excessive, it is more economical to use a second type of LSI component called a Programmable Logic Array (PLA).

A Programmable Logic Array is similar to a ROM in concept; however it does not provide full decoding of the variables and does not generates all the minterms as in the ROM. The PLA replaces decoder by group of AND gates, each of which can be programmed to generate a product term of the input variables. In PLA, both AND and OR gates have fuses at the inputs, therefore in Programmable Logic Array both AND and OR gates are programmable. Fig. 3.88 shows the Block Diagram of PLA. It consists of n inputs, output buffer with m outputs, m product terms, m sum terms, input and output buffers. The product terms constitute a group of m AND gates and the sum terms constitute a group of m OR gates, called OR matrix. Fuses are inserted between all n inputs and their complement values to each of the AND gates. Fuses are also provided between the outputs of the AND gates and the inputs of the OR gates. The third set of fuses in the output inverters allows the output function to be generated either in the AND-OR form or in the AND-OR-INVERT form. When inverter is bypassed by link we get AND-OR implementation. To get AND-OR-INVERTER implementation inverter link has to be disconnected.

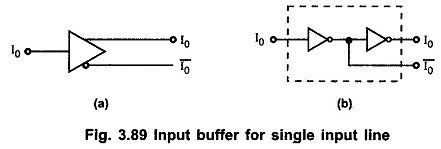
Input Buffer:

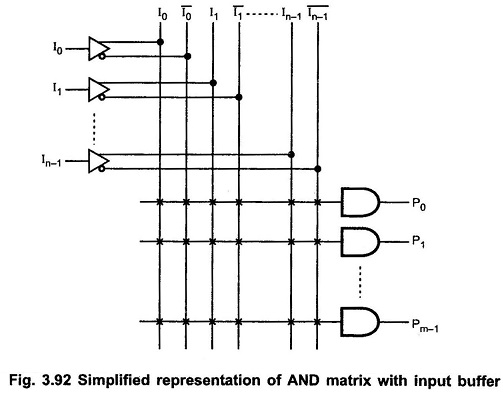
Input buffers are provided in the Programmable Logic Array to limit loading of the sources that drive the inputs. They also provide inverted and non-inverted form of inputs at its output. The Fig. 3.89 shows two ways of representing input buffer for single input.

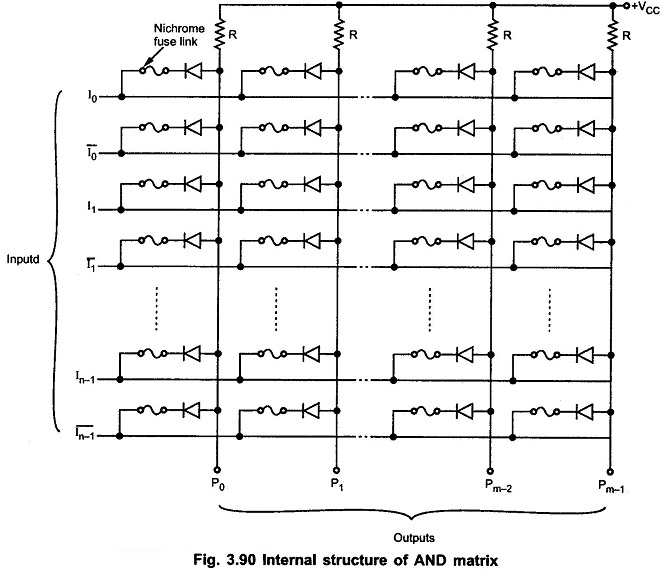
AND Matrix:

The Fig. 3.90 shows the AND matrix. It is used to form product terms. It has m AND gates with 2n inputs and m outputs, one for each AND gate. The Fig. 3.90 shows the AND gates formed by diodes and resistors structure. Each AND gate has all the input variables in complemented and uncomplemented form. There is a nichrome fuse link in series with each diode which can be burn out to disconnect particular input for that AND gate. Before programming, all fuse links are intact and the product term for each AND gate is given by

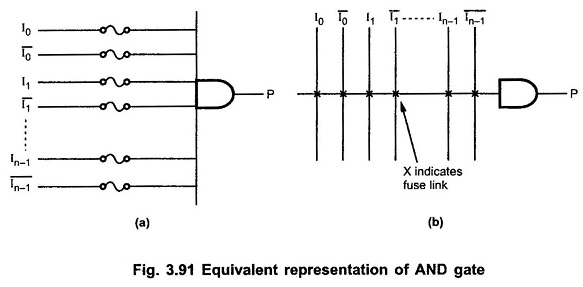
The Fig. 3.91 shows the simplified and equivalent representation of input connections for one AND gate. The array logic symbol shown in Fig. 3.91 (b) uses a single horizontal line connected to the gate input and multiple vertical lines to indicate the individual inputs. Each intersection between horizontal line and vertical line indicates the fuse connection.

The Fig. 3.92 shows the simplified representation of AND matrix with input buffer.

OR Matrix:

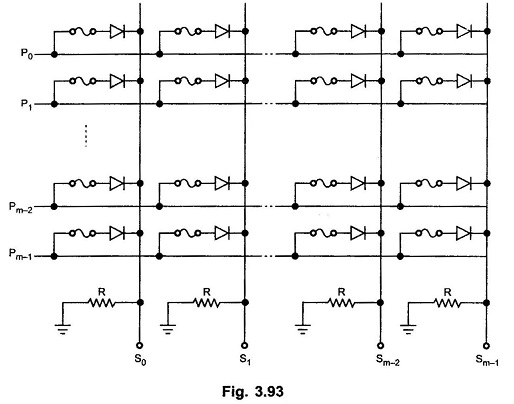
The OR matrix is provided to produce the logical sum of the product term outputs of the AND matrix. The Fig. 3.93 shows the OR gates formed by diodes and resistors, structure. Each OR gate has all the product terms as input variables. There is a nichrome fuse link in series with each diode which can be burn out to disconnect particular product term for that OR gate. Before programming, all fuse link in OR matrix are also intact and the sum term for each OR gate is given by

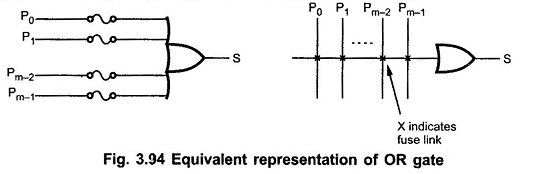
The Fig. 3.94 shows the simplified and equivalent representation of input connections for one OR gate.

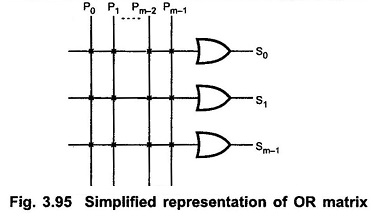
The Fig. 3.95 shows the simplified representation of OR matrix.

Invertible and Non Invertible Matrix:

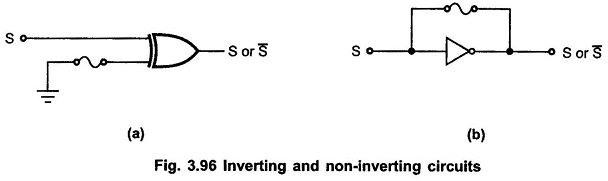
Invertible and Non Invertible Matrix provides output in the complement or uncomplemented form. The user can program the output in either complement or un-complement form as per design requirements. The typical circuits for Invertible and Non Invertible Matrix is as shown in Fig. 3.96. In both the cases if fuse is intact the output is in its uncomplemented form; otherwise output is in the complemented form.

Output Buffer:

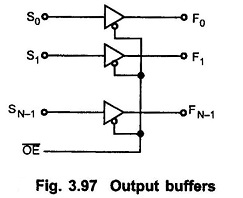
The driving capacity of PLA is increased by providing buffers at the output. They are usually TTL compatible. The Fig. 3.97 shows the tri-state, TTL compatible output buffer. The output buffer may provide totem-pole, open collector or tri-state output.

Output Through Flip-Flops:

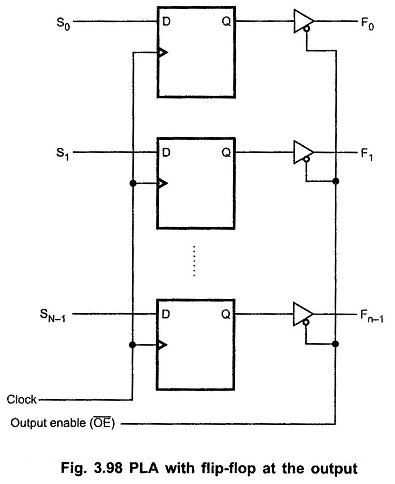
For the implementation of sequential circuits we need memory elements, flip-flops and combinational circuitry for deriving the flip-flop inputs. To satisfy both the needs some PLAs are provided with flip-flop at each output, as shown in the Fig. 3.98.

Implementation of Combination Logic Circuit using PLA:

Like ROM, PLA can be mask-programmable or field-programmable. With a mask-programmable PLA, the user must submit a PLA program table to the manufacturer. This table is used by the vendor to produce a user-made PLA that has the required internal paths between inputs and outputs. A second type of PLA available is called a field-programmable logic array, or FPLA. The FPLA can be programmed by the user by means of certain recommended procedures. FPLAs can be programmed with commercially available programmer units.