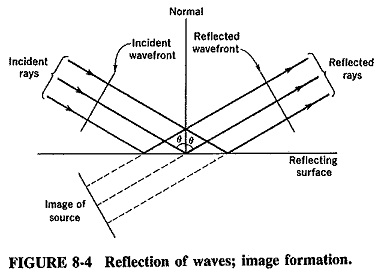
Reflection of Waves:
There is much similarity between the reflection of light by a mirror and the reflection of electromagnetic waves by a conducting medium. In both instances the angle of reflection is equal to the angle of incidence, Reflection of Waves as illustrated in Figure 8-4. Again, as with the reflection of light, the incident ray, the reflected ray and the normal at the point of incidence are in the one plane. The concept of images is used to advantage in both situations.
The proof of the equality of the angles of reflection and incidence follows the corresponding proof of what is known as the second law of reflection for light. Both proofs are based on the fact that the incident and reflected waves travel with the same velocity. There is yet another similarity here to the reflection of light by a mirror. Anyone who has been to a barber shop, in which there is a mirror behind as well as one in front, will have noticed not only that a huge number of images are present, but also that their brightness is progressively reduced. As expected, this is due to some absorption at each reflection; this also happens with radio waves.
The reflection coefficient ρ is defined as the ratio of the electric intensity of the reflected wave to that of the incident wave. It is unity for a perfect conductor or reflector, and less than that for practical conducting surfaces. The difference is a result of the absorption of energy (and also its transmission) from the wave by the imperfect conductor.
Transmission is a result of currents set up in the imperfect conductor, which in turn permit propagation within it, accompanied by refraction.
A number of other points connected with reflection must now be noted. First, it is important that the electric vector be perpendicular to the conducting surface; otherwise surface currents will be set up, and no reflection will result, in connection with waveguides. Second, if the conducting surface is curved, reflection will once again follow the appropriate optical laws which deals with parabolic and hyperbolic reflecting surfaces.
Finally, if the reflecting surface is rough, reflection will be much the same as from a smooth surface, provided that the angle of incidence is in excess of the so-called Rayleigh criterion.