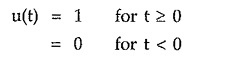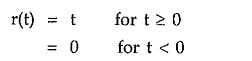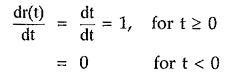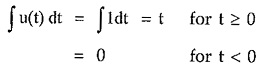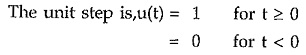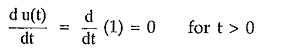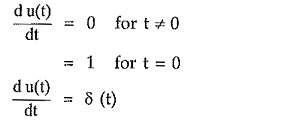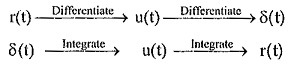Relationships Between Standard Time Function:
The Relationships between Standard Time Function contains two parts, namely
- Relation Between Unit Step and Unit Ramp
- Relation Between Unit Step and Unit Impulse
1. Relation Between Unit Step and Unit Ramp:
The unit step is given by,
while the unit ramp is given by,
Differentiating ramp function with respect to time t,
This differentiation gives, nothing but an unit step function. Thus we can write,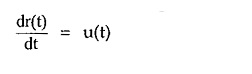
Conversely if we integrate unit step function with respect to time t we get,
This is nothing but a ramp function.
2. Relation Between Unit Step and Unit Impulse:
Differentiate unit step function with respect to time t,
Now at t = 0, the u(t) function changes from 0 to 1. Hence only at t = 0, du(t)/dt = ∞.
Thus at t = 0, du(t)/dt is nothing but an impulse of infinite magnitude and zero width having unit area under the pulse.
This is unit impulse function.
Conversely an integration of an unit impulse function results into an unit step function.![]()
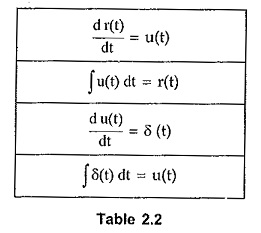
The relations can be summarised as given in the Table 2.2.
Relations between standard functions
From the above table, the ramp and impulse functions can be related as shown below,