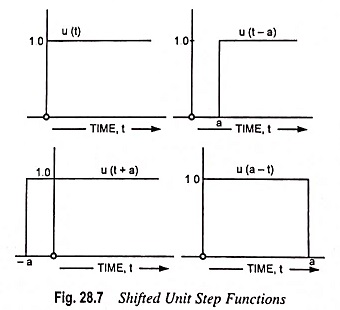
Shifted Unit Step Function:

This Shifted Unit Step Function is defined by the equation

for a step function which changes abruptly at the time t = + a. In general, the step function has unit value when the quantity (t – a), the argument of the function u, is positive, and has zero value when (t – a) is negative. This definition will apply for any form of the variable. Hence the function u (t + a) is one that changes from zero to unit value at t = – a.

Similarly the function u (a – t) is one that changes from unit to zero value (with increasing time) at the time t = a. These functions are represented in Fig. 28.7.