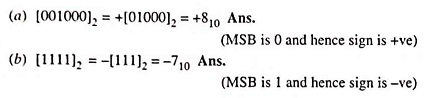Signed Binary Numbers (Definition, Conversions & Examples):
In the decimal number system, a plus (+) sign is used for denoting a positive number and a minus (-) sign for denoting a negative number. The plus sign is normally dropped, and absence of any sign means the number is positive one. This representation of numbers is called the signed Binary numbers.
In Signed binary numbers system, negative binary numbers are represented in three ways : Signed magnitude representation. 1’s complement representation and 2’s complement representation.
Signed Magnitude Representation:
In this representation an additional bit called the sign bit is placed as the MSB to the magnitude of the numbers. The ‘0’ is used for ‘+’ sign and digit (r – 1) is used for ‘-‘ sign where r is the base (radix) of the number system and it is (2 – 1) = 1 in binary system. For example in 8 bit binary number having one sign bit and seven magnitude bits, the largest positive number is 01111111 = +127 and smallest number is 11111111 = -127.
Example 44.20: Find the decimal equivalent of the following binary numbers assuming signed magnitude representation of the number. (a) 001000, (b) 1111.
Solution:
One’s Complement Representation:
In a digital work, two types of complements of binary numbers viz. 1’s complement and 2’s complement are used for complemental subtraction.
In a binary number, if each 1 is replaced by 0 and each 0 by 1, the resulting number is known as 1’s complement of first number. In fact, both numbers are complement of each other. A few examples of 1’s complement are given below for illustration
1’s Complement Subtraction:
Subtraction of binary numbers can be accomplished by using 1’s complement method, which allows us to subtract using only addition. This method of subtraction is particularly useful in arithmetic logic circuits because subtraction can be accomplished with an adder. Also the 1’s complement of a number is easily obtained by inverting each bit in the number.
1’s complement subtraction in binary can be accomplished in the same manner as 9’s complement subtraction is affected in decimal number system i.e., subtraction of a small binary number from a larger one can be accomplished by adding 1’s complement of the smaller number to the larger number and then adding the carry to the result (called an end-around carry). For subtracting a larger number from a smaller one, there is no carry, and the result is in 1’s complement form and negative. Following example will illustrate the procedure.
Example 44.21: Subtract by using (r – 1)’s complement method where r is the base of the number (100110.101)2 and (101011.01)2
Solution:
2’s Complement Representation:
The 2’s complement of a binary number is obtained by adding 1 to its 1’s complement i.e.,
2’s complement = 1’s complement + 1.
The following example illustrates the procedure.
Example 44.23: Find the 2’s complement of (i) (110110)2 and (10000)2.
Solution:
2’s Complement Subtraction:
For subtracting a smaller number from a larger one by 2’s complement subtraction method, the procedure applied is as follows :
- Determine the 2’s complement of the smaller number.
- Add the 2’s complement of the smaller number to the larger one.
- Discard the carry (there is always a carry in this case).
For subtracting a larger number from smaller one by 2’s complement subtraction method, the procedure applied is as follows:
- Determine the 2’s complement of the larger number.
- Add 2’s complement of the larger number to the smaller one.
- There is no carry. The result is in 2’s complement and is negative.
- For having result in true form, take 2’s complement and change the sign.
Both of the methods of complement subtraction have distinct advantages when implemented with logic circuits because they allow subtraction to be accomplished by using only addition. Both of the 1’s and the 2’s complements of a binary number are relatively easy to accomplish with logic circuits: and the 2’s complement has an advantage over the 1’s complement in that an end-around carry operation does not have to be performed.
Example 44.25: 11100.101 – 101.01 using 2’s complement.
Solution: