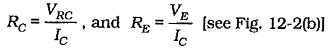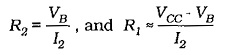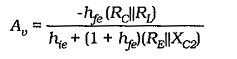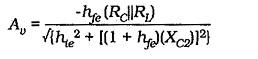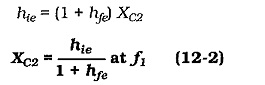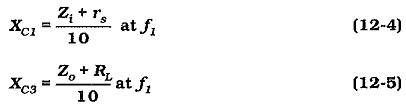Single Stage Common Emitter Amplifier Circuit:

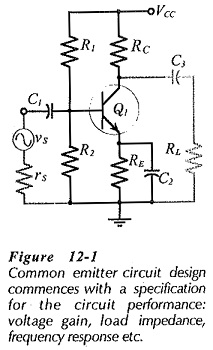
Specification – Bias circuit design for the Single Stage Common Emitter Amplifier Circuit in shown in Fig. 12-1 and ac analysis of the circuit is already explained. Design of this circuit (or any other circuit) normally commences with a specification which might list: the supply voltage, minimum voltage gain, frequency response, signal source impedance, and the load impedance.

Selection of I_C, R_C, and R_E

Designing for a particular voltage gain requires the use of ac negative feedback to stabilize the gain. The circuit shown in Fig. 12-1 has no provision for negative feedback, consequently, it is designed to achieve the largest possible voltage gain. From Eq. 6-15, the voltage gain of a Single Stage Common Emitter Amplifier Circuit,

Because A_v is directly proportional to R_C||R_L, design for the greatest voltage gain would seem to require selection of the largest possible collector resistance. However, a very large value of R_C might make the collector current too small for satisfactory transistor operation. For most small-signal transistors, I_C should not be less than 500 μA. A good minimum I_C to aim for is 1 mA. Special low-noise transistors operate with much lower collector current levels.

The transistor h_fe value is related to I_C, so I_C might be selected high to give the largest h_fe, again to achieve the greatest A_v. But, a high I_C level results in a small R_C value for a given voltage drop (V_RC). So, a high I_C level might actually result in a low A_v value, although h_fe might be relatively large.

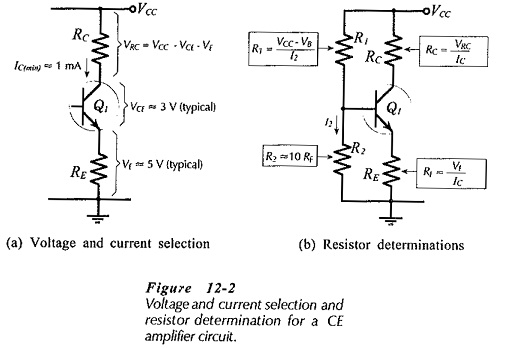
For a given level of I_C, the largest possible voltage drop across R_C gives the greatest R_C value, (R_C = V_RC/I_C). To make V_RC as large as possible, V_CE and V_E should be held to a minimum, [see Fig. 12-­2(a)]. The collector-emitter voltage should typically be around 3 V. This is large enough to ensure that the transistor operates linearly, and it also allows for a collector voltage swing of ±1 V which is usually adequate for a small-signal amplifier. Another consideration in selecting R_C is that there is nothing to be gained by making R_C larger than R_L. In fact, R_C should normally be very much smaller than R_L, so that R_L has little effect on the circuit voltage gain.

For good bias stability, the emitter resistor voltage drop (V_E) should be much larger than the base-emitter voltage (V_BE). This is because V_E = V_B – V_BE, and when V_E ≫ V_BE, V_E will be only slightly affected by any variation in V_BE (due to temperature change or other effects). Consequently, I_E and I_C remain fairly stable at I_C ≈ I_E = V_E/R_E. A minimum V_E of 5 V gives good bias stability in most circumstances, [see Fig. 12-2 (a)]. With supply voltages less than 10 V, V_E might have to be reduced to 3 V to allow for reasonable levels of V_CE and V_RC. Normally, an emitter resistor voltage drop less than 3 V is likely to produce poor bias stability.

Once V_E, V_CE, and I_C are selected, V_RC is determined as,

Then, R_C and R_E are calculated,

Bias Resistors:

As we know already, selection of the voltage divider current (I₂) as I_C/10 gives good bias stability and reasonably high input resistance. Where the input resistance is not important, I₂ may be made equal to I_C for excellent bias stability. The bias resistors are calculated as,

Selecting R₂ = 10 R_E gives I₂ ≈ I_C/10, [Fig. 12-2(b)]. The precise level of I₂ can be calculated as I₂ =V_B/R₂, and this can be used in the equation for R₁.

Bypass Capacitor:

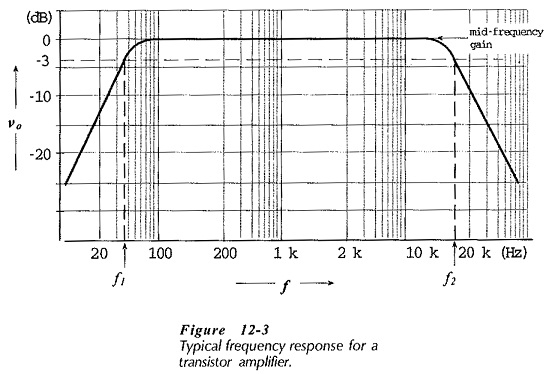
All capacitors should be selected to have the smallest possible capacitance value, both to minimize the physical size of the circuit and for economy (large capacitors are the most expensive). Because each capacitor has its highest impedance at the lowest operating frequency, the capacitor values are calculated at the lowest signal frequency that the circuit is required to amplify. This frequency is the circuit lower cutoff frequency, or low 3 dB frequency (f₁), (see Fig. 12-3).

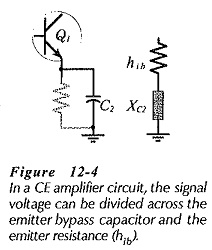
Bypass capacitor C₂ in Fig. 12-1 is normally the largest capacitor in the circuit, so C₂ is selected to set f₁ at the desired frequency. Voltage gain was developed for a Single Stage Common Emitter Amplifier Circuit with an unbypassed emitter resistor (R_E). Rewriting the equation to include X_C2 in parallel with R_E gives

Normally R_E ≫ X_C2, so R_E can be omitted. Also, X_C2 is capacitive,

so,

when h_fe = (1 + h_fe) X_C2,

Therefore, at f₁,

At f₁,

Equations 12-2 and 12-3 give the smallest value for the bypass capacitor. When selecting a standard value for the capacitor, the next larger value should be chosen. This will give a cutoff frequency slightly lower than the  f₁ value used in the calculations.

It is important to note that the emitter bypass capacitor is calculated in terms of the resistance ‘seen looking into’ the transistor emitter terminal (the resistance in series with C₂). The capacitor value is not determined in relation to the value of the emitter resistor (R_E).

Coupling Capacitors:

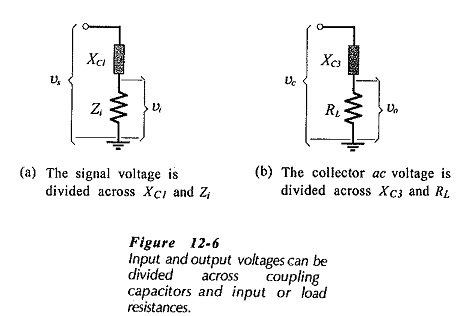
The coupling capacitors (C₁ and C₃ in Fig. 12-1) should have a negligible effect on the frequency response of the circuit. Figure 12-­6(a) illustrates the fact that X_C1 and Z_i constitute a voltage divider If X_C1 is too large, the circuit ac input voltage (v_i) will be significantly smaller than the signal voltage (v_s). Similarly, X_C3 and R_L attenuate the ac voltage at the transistor collector, so that the ac output voltage (v_o) can be smaller than the ac collector voltage (v_o), [Fig. 12-6(b)]. To minimize the effects of C₁ and C₃, the reactance of each coupling capacitor is selected to be approximately equal to one-tenth of the impedance in series with it at the lowest operating frequency for the circuit (f₁).

Usually, R_L ≫ Z_o, and often Z_i ≫ r_s, so that Z_o and r_s can be omitted in Equations 12-4 and 12-5. Once again, the equations give minimum capacitance values, so that the next larger standard values should always be selected for C₁ and C₃.

Equations 12-4 and 12-5 give an impression that approximately 10% of the signal and output voltages are lost across C₁ and C₃. This would be true if the quantities were resistive. However, X_C1 and X_C3 are capacitive while Z_i and R_L are usually resistive. So, when the actual loss is calculated, it is found to be only around 0.5% for each capacitor.

Another approach to the selection of coupling capacitors is to make X_C1 = Z_i  at two octaves below f₁.

The output coupling capacitor is then determined by making impedance of C₃ equal to R_L at two octaves below f₁/4.

When Equations 12-6 and 12-7 are used to determine the values of the coupling capacitors, it can be shown that the capacitor attenuation effects are less than 5% of A_v.

Shunting Capacitor:

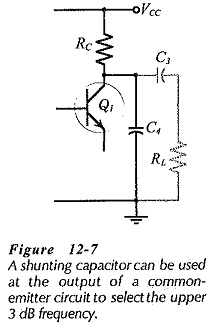
Sometimes an amplifier is required to have a particular upper cutoff frequency, (f₂ in Fig. 12-3). The transistor must be selected to have a much higher cutoff frequency than f₂. The upper cutoff frequency for the circuit can then be set by connecting a small capacitor from the transistor collector terminal to ground, (C₄ in Fig. 12-7).