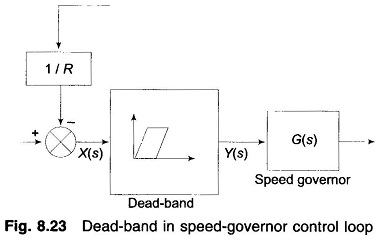
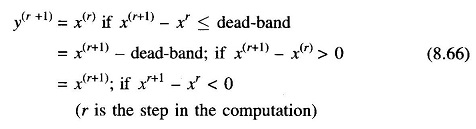Speed Governor Dead Band and its Effect on AGC:
The effect of the Speed Governor Dead Band is that for a given position of the governor control valves, an increase/decrease in speed can occur before the position of the valve changes. The governor dead-band can materially affect the system response. In AGC studies, the dead-band effect indeed can be significant, since relatively small signals are under considerations.
The Speed Governor characteristic, though non-linear, has been approximated by linear characteristics in earlier analysis. Further, there is another non-linearity introduced by the dead-band in the governor operation. Mechanical friction and backlash and also valve overlaps in hydraulic relays cause the governor dead-band. Due to this, though the input signal increases, the Speed Governor may not immediately react until the input reaches a particular value.
Similar action takes place when the input signal decreases. Thus the governor dead-band is defined as the total magnitude of sustained speed change within which there is no change in valve position. The limiting value of dead-band is specified as 0.06%. One of the effects of governor dead-band is to increase the apparent steady-state speed regulation R.
The effect of the dead-band may be included in the speed governor control loop block diagram as shown in Fig. 8.23. Considering the worst case for the dead-band, (i.e., the system starts responding after the whole dead-band is traversed) and examining the dead-band block in Fig. 8.23, the following set of equations completely define the behavior of the dead-band.
Reference considers the effect of governor dead-band nonlinearity by using the describing function approach and including the linearized equations in the state space model.
The presence of governor dead-band makes the dynamic response oscillatory. It has been seen that the governor dead-band does not influence the selection of integral controller gain settings in the presence of GRCs. In the presence of GRC and dead band even for small load perturbation, the system becomes highly non-linear and hence the optimization problem becomes rather complex.