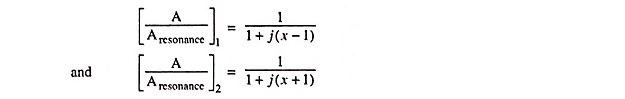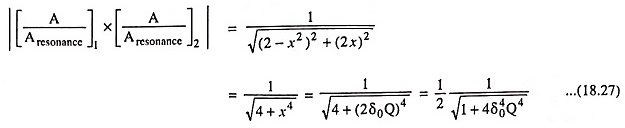Stagger Tuned Amplifier – Circuit diagram and its Workings:
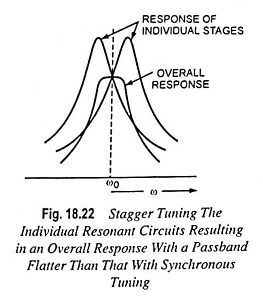
In order to increase bandwidth, double tuned amplifiers are preferred, but their alignment is difficult. A much better overall response can be had by stagger tuning, as illustrated in Fig. 18.22.
If two or more tuned circuits are cascaded and tuned to the same frequency, it is called the synchronous tuning. The overall bandwidth is reduced. On the other hand, if the tuned circuits are cascaded and they are tuned to different frequencies, it is possible to have increased bandwidth with more desirable characteristics (i.e., flat passband with steeper sides). This technique is called the stagger tuning.
Operation:
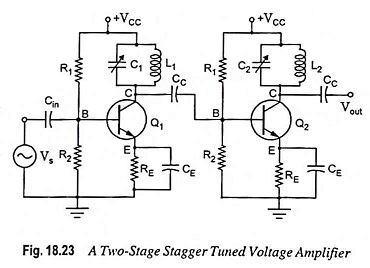
A two-stage stagger tuned voltage amplifier is shown in Fig. 18.23. In stagger tuned circuits, two single tuned cascaded amplifiers having a certain bandwidth are taken and the resonant frequencies of the two tuned circuits are so adjusted that they are separated by an amount equal to the bandwidth of each stage. Stagger tuned amplifiers are usually designed so that the overall response exhibits maximum flatness around the center frequency f0. It needs a number of tuned circuits operating in union. If more number of stages are employed flatter will be the passband and steeper will be the gain fall of outside the passband. Because of stagger tuning there is a loss of voltage gain. The overall frequency response of a stagger tuned amplifier is obtained by adding individual response together. Since the resonant frequencies of different tuned circuits are displaced or staggered, they are referred to as stagger tuned amplifier.
Advantages and Disadvantages:
The main advantage of stagger tuned amplifier is increased bandwidth. Its drawbacks are reduced selectivity and critical tuning of many tank circuits. They are used in RF amplifier stage in radio receivers.
The resultant staggered pair will have a bandwidth √2 times that of each individual single tuned circuits. The overall selectivity function will be identical in form with that of a single stage double tuned amplifier. The gain of the single tuned amplifier is given as
where x = 2Qeδ
As bandwidth is given as B = f0/Qe and under 3-dB frequency condition δ = 1/2Qe, the equation for bandwidth can be written as
B = 2δf0
Since one stage is tuned to a frequency δ0f0 below f0 and the other stage is tuned to a frequency δ0f0 above f0, the corresponding selectivity function of the circuits are
Multiplying the relative gains of the two amplifiers, we have the overall gain function as
The magnitude of the resultant function is
where δ0 is the value of δ referred to new frequency f0 and Q is the value of Qe for each circuit referred to ω0. The above Eq. (18.27), if compared with that of double tuned amplifier, we find that the nature of variation is identical.