Twigs and Links:

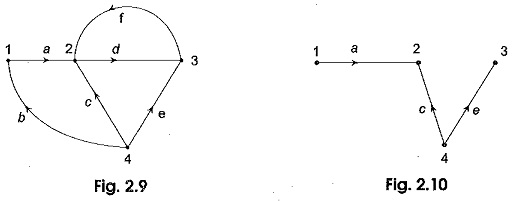
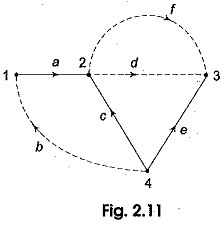
Twigs and Links – The branches of a tree are called its ‘twigs’. For a given graph, the complementary set of branches of the tree is called the co-tree of the graph. The branches of a co-tree are called links, i.e. those elements of the connected graph that are not included in the tree links and form a subgraph. For example, the set of  branches (b, d, f) represented by dotted lines in Fig. 2.11 form a co-tree of the graph in,Fig, 2.9 with respect to the tree in Fig. 2.10.

The branches a, c and e are the twigs while the branches b, d and f are the links of this tree. It can be seen that for a network with b branches and n nodes, the number of twigs for a selected tree is (n — 1) and the number of links I with respect to this tree is (b – n + 1). The number of twigs (n — 1) is known as the tree value of the graph. It is also called the rank of the tree. If a link is added to the tree, the resulting graph contains one closed path, called a loop. The addition of each subsequent link forms one or more additional loops. Loops which contain only one link are independent and are called basic loops.