V Shift and I Shift Method:
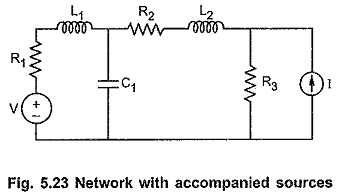
V Shift and I Shift Method – A voltage source with a passive branch in series with it is called an accompanied voltage source. Similarly a current source with a passive branch in parallel with it is called an accompanied current source. Such accompanied voltage and current sources are shown in the Fig. 5.23.
While drawing a graph, such a accompanied source can be replaced by their internal impedances. If their internal impedances are not given, then replace voltage source by short circuit and current source by open circuit.
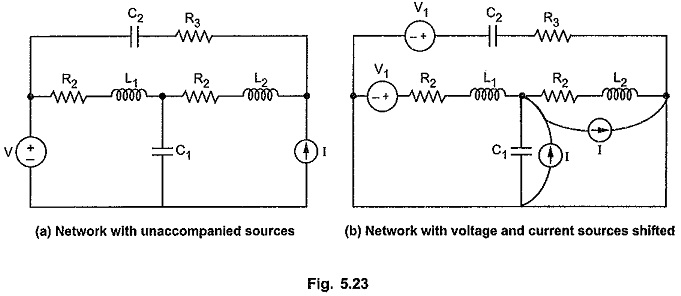
But if in the network, the sources are unaccompanied, then it is very difficult to select number of unknowns in terms of number of branches if the sources are treated as separate branches. Consider a network shown in the Fig. 5.23 (a).
We can get some equivalence between the networks with and without accompanied sources by using source shifting technique in the network with unaccompanied sources. Thus by using source shifting technique unaccompanied source can be made accompanied source.
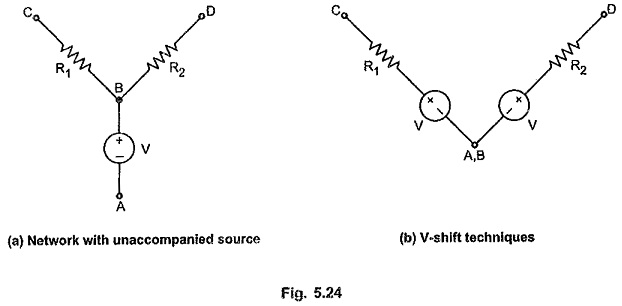
Consider a network shown in the Fig. 5.24 (a)
In such a cases, short terminals A and B and push voltage source V through the node in series with passive element R1 and R2. This makes unaccompanied, accompanied one. This is known as voltage source shifting technique or V-shift technique. The networks shown in the Fig. 5.25 (a) and (b) are equivalent as far as KVL is concerned.
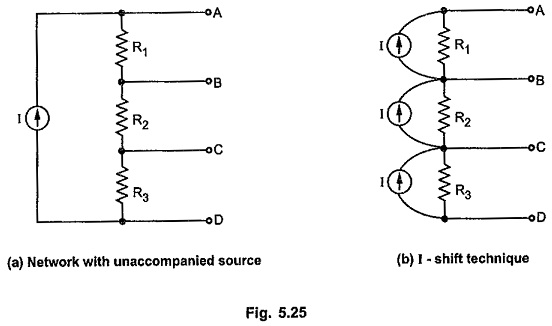
Consider a network shown in the Fig. 5.25 (a) in which current source is unaccompanied.
In such a cases, remove original current source and introduce additional current sources which are identical to original one across each branch as shown in the Fig. 5.25 (b). The technique is known as current source shifting technique or I-shift technique. The networks shown in the Fig. 5.25 (a) and (b) are equivalent as far as KCL is concerned.
Thus V-shift and I-shift techniques are most useful in making all the sources as accompanied sources and it is most suitable to consider all sources as accompanied for writing loop and node equations.