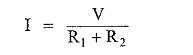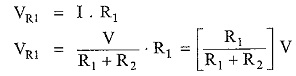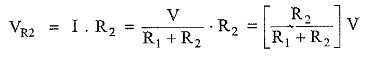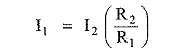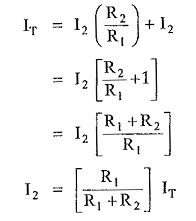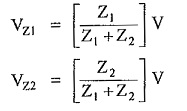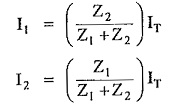Voltage and Current Divider Rule:
Voltage and Current Divider Rule is explained by two conditions, namely
- Voltage Division in Series Circuit of Resistors
- Current Division in Parallel Circuit of Resistors
Voltage Division in Series Circuit of Resistors:
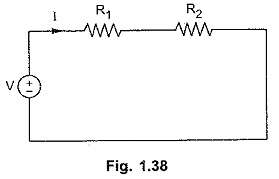
Consider a series circuit of two resistors R1 and R2 connected to source of V volts is shown in Fig. 1.38.
As two resistors are connected in series, the current flowing through both the resistors is same, i.e. I. Then applying KVL, we get,
V = I R1 + I R2
Total voltage applied is equal to the sum of voltage drops VR1 and VR2 across R1 and R2 respectively.
VR1 = I . R1
Similarly,
So this circuit is a Voltage Divider Circuit. So in general, voltage drop across any resistor, or combination of resistors, in a series circuit is equal to the ratio of that resistance value to the total resistance, multiplied by the source voltage.
Current Division in Parallel Circuit of Resistors:
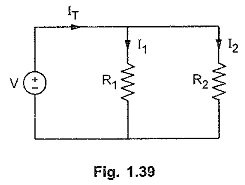
Consider a parallel circuit of two resistors R1 and R2 connected across a source of V volts is shown in Fig. 1.39.
Current through R1 is I1 and R2 is I2, while total current drawn from source is IT.
IT = I1 + I2
But
i.e. V = I1 R1 = I2 R2
Substituting value of I1 in IT,
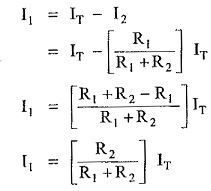
Now
In general, the current in any branch is equal to the ratio of opposite branch resistance to the total resistance value, multiplied by the total current in the circuit.
Note : The above results of both Voltage and Current Divider Rule sections are equally applicable if there exists in network, the impedances in series or parallel instead of pure resistances R1 and R2.
If there exists alternating voltage source of V volts and two impedances Z1 and Z2 in series then voltage division is,
While in a parallel circuit of two impedances, the current division is given by,
It must be remembered that in alternating circuits multiplication and division must be carried out in polar form while addition and subtraction must be carried out in rectangular form.