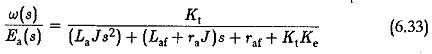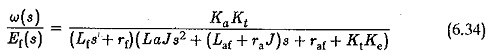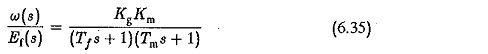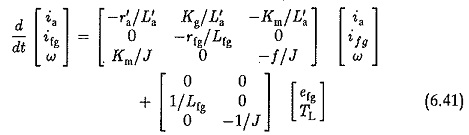Ward Leonard Drive Transfer Function:

In the classical Ward Leonard Drive Transfer Function, the dc drive motor having constant excitation is supplied from a variable voltage generator, as shown in Fig. 6.9. The generator is driven at constant speed. The field current of the dc generator is varied by varying the field voltage to have variable voltage at the terminals, which is ultimately fed to the motor. A transfer function relating the speed of the motor and generator field voltage is required.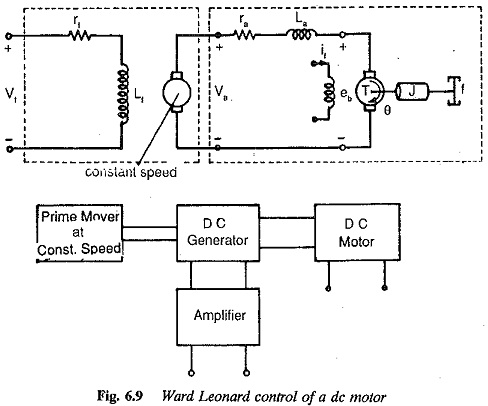

The system equations are

The voltage induced in the armature of the generator is given by

where K_a is a constant which includes the constancy of generator speed and the proportionality constant between field current and air gap flux. As usual the effects of saturation are neglected. Eliminating i_fg from Eq. 6.30 we have

The transfer function between the armature voltage and field voltage of the generator is given by

The transfer function of the armature controlled motor is

Combining Eqs 6.32 and 6.33, we have

Neglecting the effects of L_a the transfer function simplifies in the second order to

where

K_g = (K_a/r_f) generator gain constant

T_f = L_f/r_f generator field time constant

K_m=K_t/(r_af+K_tK_e) motor gain constant

T_m = r_aJ/(r_af+K_tK_e) motor time constant

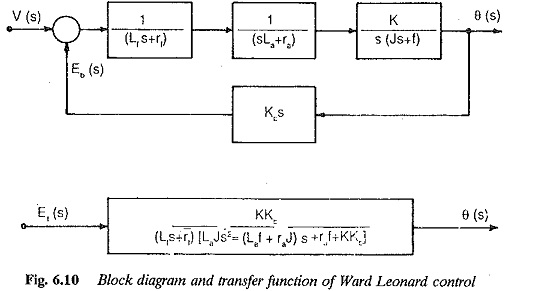
The block diagrams of a generator and a motor are shown in Fig. 6.10.

Alternately: The equations of the system may be derived in the state vari­able form taking i_f,i_a and ω as the state variables. A signal flow graph may be drawn to represent these equations. Using Mason’s gain formula the transfer function may be derived.

Using the schematic of Fig. 6.9 representing a Ward Leonard speed control system we have for the generator field circuit

which can be rearranged as

For the loop of armatures the circuit equation is given by

e_a is the voltage induced in the armature of the generator and is given by K_gⁱ_fg.

r′_a and L′_a include resistance and inductance of both generator and motor armatures respectively.

e_m is the back emf of the motor given by K_mω. Substituting in Eq. (6.37) and rearranging the terms we have

The torque balance equation gives the dynamics of the motor. It is

Rearranging the terms we have

Equations 6.40 are the state equations of the system and given in matrix ro­tation as