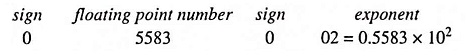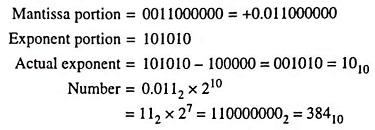What is a Floating Point Number?
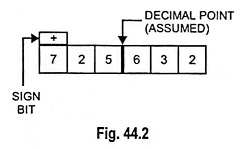
The real numbers considered so far were represented in what is known as fixed point notation. In such notation, the position of the decimal is fixed for a fixed number of bits. For example, a number say 725.632 can be stored in a 6 bit register as shown in Fig. 44.2.
The scientific calculations involve very large and very small numbers which cannot be expressed in fixed point notation.
In decimal system, very large and very small numbers are expressed in scientific notation, known as floating point notation, by stating a number (mantissa) and an exponent of 10. Examples are 3.02 x 108, 5.83 x 10-6 or 8.25 x 10-27.
A floating point number N can be represented in the form N = F x be, where F is any number of base b and e is exponent. For example the decimal number 55.83 can be represented as 0.5583 x 102 or 558.3 x 10-1 or 5583 x 10-2. The number F x be is called a normalized floating point number if 1/b < F < 1. Therefore the above decimal number 55.83 is represented 0.5583 x 102 (1/10 < 0.5583 < 1) as normalized floating point number.
The floating point representation of a number have two parts, the first part is signed, fixed point number called the mantissa and the second part is signed exponent. For example, 55.83 is represented as
Likewise binary numbers (mantissa) can also be expressed by a number and an exponent of 2. This representation of binary number is called Floating point number. In a 16 bit computer 10 bits are mantissa and remaining 6 bits are exponent. The mantissa is written in 2’s complement form and therefore MSB is taken as sign bit. The binary point is placed after this bit (or it may be placed at the given radix point position). The remaining 6 bits are the exponent component representing 0 to 63. The binary number 1000002 (32)10 is added to the desired exponent for representing negative exponents. It is called the excess-32 exponent.
Example 44.29: Find out the decimal number for a floating point number 0011000000101010.
Solution: